题目内容
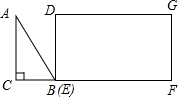
如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°;四边形DEFG为矩形,DE=2| 3 |
(1)求AC的长度;
(2)将Rt△ABC以每秒1 cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止移动,设Rt△ABC与矩形DEFG重叠部分的面积为y,请求出重叠面积y(cm2)与移动时间x(s)的函数关系式(时间不包括起始与终止时刻);
(3)在(2)的基础上,当Rt△ABC移动至重叠部分的面积y=
| 3 |
| 2 |
| 3 |
 并使点C与点C’重合,请求出翻折后Rt△ABC’与矩形DEFG重叠部分的周长.
并使点C与点C’重合,请求出翻折后Rt△ABC’与矩形DEFG重叠部分的周长.
分析:(1)在直角三角形ABC中,根据BC的长和∠A的与余切值即可求出AC的长;
(2)本题要找出几个关键点:当C与B重合、A与D重合时,x=2.当B与F重合时,x=6;当C与F重合时,x=8;因此本题可分三种情况:
①当0<x<2时,此时重合部分是个直角三角形且与三角形ABC相似,可用它们的形似比求出重合部分的面积,
②当2≤x≤6时,重合部分是三角形ACB,因此其面积就是三角形ABC的面积,
③当6<x<8时,重合部分是个直角梯形,可参照①的思路进行求解;
(3)可将y的值分别代入(2)的三种情况中,求出符合条件的x的值,然后用相似三角形和解直角三角形的相关知识进行求解即可.
(2)本题要找出几个关键点:当C与B重合、A与D重合时,x=2.当B与F重合时,x=6;当C与F重合时,x=8;因此本题可分三种情况:
①当0<x<2时,此时重合部分是个直角三角形且与三角形ABC相似,可用它们的形似比求出重合部分的面积,
②当2≤x≤6时,重合部分是三角形ACB,因此其面积就是三角形ABC的面积,
③当6<x<8时,重合部分是个直角梯形,可参照①的思路进行求解;
(3)可将y的值分别代入(2)的三种情况中,求出符合条件的x的值,然后用相似三角形和解直角三角形的相关知识进行求解即可.
解答:解:(1)AC=BC•cot∠A=2
(cm);
(2)如图(1)当0<x<2时
=(
)2,
∴y=
×
×2×2
即y=
x2;
当2≤x≤6时y=S△ABC=2
.
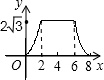
如图(2)当6<x<8时,AB交FG于H,
=(
)2
∴S△FHB=
(x-6)2
∴y=S△ABC-S△FHB=2
-
(x-6)2=-
x2+6
x-16
综上所述:y与x的函数关系式为y=
;
(3)当0<x<2时,
x2=
,
∴x=
.
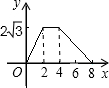
如图(3)AB交DE于点M,ACˊ交DE于点N,
则∠AMN=∠CAB=∠BACˊ=30°
∴MN=AN
在Rt△MEB中,MB=2BE=2
∴重叠部分的周长=MN+NC'+C'B+BM=AN+N'C+C'B+BM=AC'+BC'+BM=2
+2+2
=4
+2(cm)
当6<x<8时,令y=
,则2
-
(x-6)2=
∴(x-6)2=1
∴x1=7,x2=5(舍去)
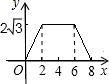
如图(4)Rt△MFB中FB=7-6=1
∴MF=1×cot30°=
,AM=MB=2
设MN=AN=a,则NG=
∴
+a+
=2
∴a=
∴重叠部分周长=C△AMN=2a+AM=
+2(cm)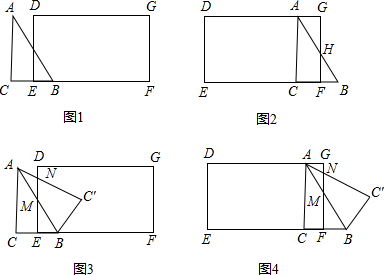
| 3 |
(2)如图(1)当0<x<2时
| y |
| S△ABC |
| x |
| 2 |
∴y=
| x2 |
| 4 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
当2≤x≤6时y=S△ABC=2
| 3 |
如图(2)当6<x<8时,AB交FG于H,
| S△FHB |
| S△ABC |
| x-6 |
| 2 |
∴S△FHB=
| ||
| 2 |
∴y=S△ABC-S△FHB=2
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
综上所述:y与x的函数关系式为y=
|
(3)当0<x<2时,
| ||
| 2 |
| 3 |
∴x=
| 3 |
如图(3)AB交DE于点M,ACˊ交DE于点N,
则∠AMN=∠CAB=∠BACˊ=30°
∴MN=AN
在Rt△MEB中,MB=2BE=2
| 3 |
∴重叠部分的周长=MN+NC'+C'B+BM=AN+N'C+C'B+BM=AC'+BC'+BM=2
| 3 |
| 3 |
| 3 |
当6<x<8时,令y=
| 3 |
| 2 |
| 3 |
| 3 |
| ||
| 3 |
3
| ||
| 2 |
∴(x-6)2=1
∴x1=7,x2=5(舍去)
如图(4)Rt△MFB中FB=7-6=1
∴MF=1×cot30°=
| 3 |
设MN=AN=a,则NG=
| a |
| 2 |
∴
| a |
| 2 |
| 3 |
| 3 |
∴a=
2
| ||
| 3 |
∴重叠部分周长=C△AMN=2a+AM=
4
| ||
| 3 |

点评:本题主要考查了直角三角形和矩形的性质、图形的翻折变换、二次函数的应用等知识,要注意(2)(3)小题要分类讨论,不要漏解.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
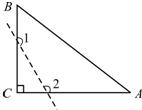 10、已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
10、已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )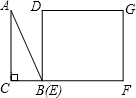 如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,
如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,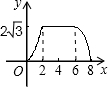
 已知如图:△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.设点Q为抛物线上点P至点B之间的一动点,连接PQ并延长交BC于点E,连接BQ并延长交AC于点F,则FC(AC+EC)=
已知如图:△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.设点Q为抛物线上点P至点B之间的一动点,连接PQ并延长交BC于点E,连接BQ并延长交AC于点F,则FC(AC+EC)=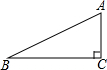 如图,△ABC为直角三角形,AC=3cm,BC=4cm,AB=5cm,将△ABC沿CB方向平移3cm,则边AB所经过的平面面积为
如图,△ABC为直角三角形,AC=3cm,BC=4cm,AB=5cm,将△ABC沿CB方向平移3cm,则边AB所经过的平面面积为