题目内容
(2007•遵义)某中学准备改造面积为1080m2的旧操场,现有甲、乙两个工程队都想承建这项工程.经协商后得知,甲工程队单独改造这操场比乙工程队多用9天;乙工程队每天比甲工程队多改造10m2;甲工程队每天所需费用160元,乙工程队每天所需费用200元.(1)求甲乙两个工程队每天各改造操场多少平方米?
(2)在改造操场的过程中,学校要委派一名管理人员进行质量监督,并由学校负担他每天25元的生活补助费,现有以下三种方案供选择.
第一种方案:由甲单独改造;
第二种方案:由乙单独改造;
第三种方案:由甲、乙一起同时进行改造;
你认为哪一种方案既省时又省钱?试比较说明.
【答案】分析:用二元一次方程组解决问题的关键是找到2个合适的等量关系,本题中2个等量关系为:“甲工程队单独改造这操场比乙工程队多用9天”和“乙工程队每天比甲工程队多改造10m2.”根据这两个等量关系可列出方程组.
解答:解:(1)设甲乙两个工程队每天各改造操场x,y平方米,
则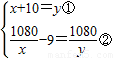
解得x=30,y=40
答:甲乙两个工程队每天各改造操场30平方米和40平方米.
(2)由甲单独改造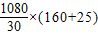 =6660;
=6660;
由乙单独改造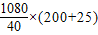 =6075;
=6075;
由甲、乙一起同时进行改造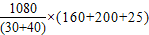 =5940
=5940
所以,甲乙合作最省钱.
点评:解题关键是弄清题意,合适的等量关系:“甲工程队单独改造这操场比乙工程队多用9天”和“乙工程队每天比甲工程队多改造10m2.”列出方程组.
解答:解:(1)设甲乙两个工程队每天各改造操场x,y平方米,
则
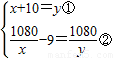
解得x=30,y=40
答:甲乙两个工程队每天各改造操场30平方米和40平方米.
(2)由甲单独改造
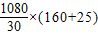 =6660;
=6660;由乙单独改造
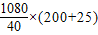 =6075;
=6075;由甲、乙一起同时进行改造
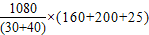 =5940
=5940所以,甲乙合作最省钱.
点评:解题关键是弄清题意,合适的等量关系:“甲工程队单独改造这操场比乙工程队多用9天”和“乙工程队每天比甲工程队多改造10m2.”列出方程组.

练习册系列答案
相关题目