题目内容
某环形道路上顺时针排列着4所中学:A1,A2,A3,A4,它们顺次有彩电15台,8台,5台,12台.为使各校的彩电数相同,允许一些中学向相邻中学调出彩电.问怎样调配才能使调出的彩电台数最小?并求调出彩电的最小总台数.
设A1中学调给A2彩电x1台(若x1<0,则认为是A2,向A1调出|x1|台),A2中学调给A3彩电x2台,A3调给A4x3台,A4调给A1x4台.
∵共有40台彩电,平均每校10台,
∴15-x1+x4=10,8-x2+x1=10,5-x3+x2=10,12-x4+x3=10,
∴x4=x1-5,x1=x2+2,x2=x3+5,x3=x4-2,x3=(x1-5)-2=x1-7,x2=(x1-7)+5=x1-2.
本题即求y=|x1|+|x2|+|x3|+|x4|=|x1|+|x1-2|+|x1-7|+|x1-5|的最小值,其中x1是满足-8≤x1≤15的整数.
设x1=x,并考虑定义在-8≤x≤15上的函数:y=|x|+|x-2|+|x-7|+|x-5|,
当2≤x≤5时,y取最小值10,
即当x1=2,3,4,5时,|x1|+|x1-2|+|x1-7|+|x1-5|取到最小值10.
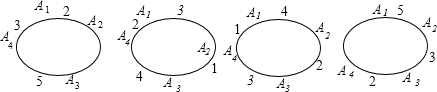
从而调出彩电的最小台数为10,调配方案有如下4种:
∵共有40台彩电,平均每校10台,
∴15-x1+x4=10,8-x2+x1=10,5-x3+x2=10,12-x4+x3=10,
∴x4=x1-5,x1=x2+2,x2=x3+5,x3=x4-2,x3=(x1-5)-2=x1-7,x2=(x1-7)+5=x1-2.
本题即求y=|x1|+|x2|+|x3|+|x4|=|x1|+|x1-2|+|x1-7|+|x1-5|的最小值,其中x1是满足-8≤x1≤15的整数.
设x1=x,并考虑定义在-8≤x≤15上的函数:y=|x|+|x-2|+|x-7|+|x-5|,
当2≤x≤5时,y取最小值10,
即当x1=2,3,4,5时,|x1|+|x1-2|+|x1-7|+|x1-5|取到最小值10.
从而调出彩电的最小台数为10,调配方案有如下4种:


练习册系列答案
相关题目
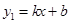 与
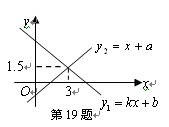
与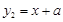 的图象如图,下列结论中:①一元二次方程组
的图象如图,下列结论中:①一元二次方程组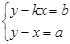 的解为
的解为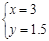 ;②关于x的不等式x+a>kx+b的解集为x<3;③k<0,
;②关于x的不等式x+a>kx+b的解集为x<3;③k<0,