题目内容
先阅读下面材料,再回答问题.
一般地,如果函数y的自变量x在a<x<b范围内,对于任意x1,x2,当a<x1<x2<b时,总是有y1<y2(yn是与xn对应的函数值),那么就说函数y在a<x<b范围内是增函数.
例如:函数y=x2在正实数范围内是增函数.
证明:在正实数范围内任取x1,x2,若x1<x2,
则y1-y2=x12-x22=( x1-x2)( x1+x2)
因为x1>0,x2>0,x1<x2
所以x1+x2>0,x1-x2<0,( x1-x2)( x1+x2)<0
即y1-y2<0,亦即y1<y2,也就是当x1<x2时,y1<y2.
所以函数y=x2在正实数范围内是增函数.
问题:
(1)下列函数中.①y=-2x(x为全体实数);②y=-
(x>0);③y=
(x>0);在给定自变量x的取值范围内,是增函数的有______.
(2)对于函数y=x2-2x+1,当自变量x______时,函数值y随x的增大而增大.
(3)说明函数y=-x2+4x,当x<2时是增函数.
一般地,如果函数y的自变量x在a<x<b范围内,对于任意x1,x2,当a<x1<x2<b时,总是有y1<y2(yn是与xn对应的函数值),那么就说函数y在a<x<b范围内是增函数.
例如:函数y=x2在正实数范围内是增函数.
证明:在正实数范围内任取x1,x2,若x1<x2,
则y1-y2=x12-x22=( x1-x2)( x1+x2)
因为x1>0,x2>0,x1<x2
所以x1+x2>0,x1-x2<0,( x1-x2)( x1+x2)<0
即y1-y2<0,亦即y1<y2,也就是当x1<x2时,y1<y2.
所以函数y=x2在正实数范围内是增函数.
问题:
(1)下列函数中.①y=-2x(x为全体实数);②y=-
| 2 |
| x |
| 1 |
| x |
(2)对于函数y=x2-2x+1,当自变量x______时,函数值y随x的增大而增大.
(3)说明函数y=-x2+4x,当x<2时是增函数.
(1)①y=-2x,
∵k=-2<0,
∴x在全体实数范围内y随x的增大而减小;
②y=-
(x>0),
∵k=-2<0,
∴x>0时,y随x的增大而增大;
③y=
(x>0),
∵k=1>0,
∴x>0时,y随x的增大而减小,
综上所述,增函数只有②;
(2)二次函数y=x2-2x+1的对称轴为x=-
=-
=1,
∵二次函数开口向上,
∴自变量x>1时,函数值y随x的增大而增大;
(3)证明:设x1<x2<2,
则y1-y2=(-x12+4x1)-(-x22+4x2),
=-x12+x22+4x1-4x2,
=-(x1-x2)(x1+x2)+4(x1-x2),
=(x1-x2)(4-x1-x2),
∵x1<x2<2,
∴-x1>-x2>-2,x1-x2<0,
∴4-x1-x2>0,
∴(x1-x2)(4-x1-x2)<0,
即y1-y2<0,
亦即y1<y2,
也就是当x1<x2<2时,y1<y2,
所以函数y=x2在正实数范围内是增函数.
∵k=-2<0,
∴x在全体实数范围内y随x的增大而减小;
②y=-
| 2 |
| x |
∵k=-2<0,
∴x>0时,y随x的增大而增大;
③y=
| 1 |
| x |
∵k=1>0,
∴x>0时,y随x的增大而减小,
综上所述,增函数只有②;
(2)二次函数y=x2-2x+1的对称轴为x=-
| b |
| 2a |
| -2 |
| 2×1 |
∵二次函数开口向上,
∴自变量x>1时,函数值y随x的增大而增大;
(3)证明:设x1<x2<2,
则y1-y2=(-x12+4x1)-(-x22+4x2),
=-x12+x22+4x1-4x2,
=-(x1-x2)(x1+x2)+4(x1-x2),
=(x1-x2)(4-x1-x2),
∵x1<x2<2,
∴-x1>-x2>-2,x1-x2<0,
∴4-x1-x2>0,
∴(x1-x2)(4-x1-x2)<0,
即y1-y2<0,
亦即y1<y2,
也就是当x1<x2<2时,y1<y2,
所以函数y=x2在正实数范围内是增函数.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 先阅读下面材料,再解答所提出的问题
先阅读下面材料,再解答所提出的问题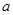 与
与 的大小,可先求出
的大小,可先求出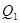 元,乙两次购买粮食的平均单价为
元,乙两次购买粮食的平均单价为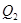 元,
元,