题目内容
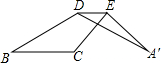如图，将△ABC沿着它的中位线DE折叠后，点A落到点A’，若∠C=120°，∠A=26°，则
∠A′DB的度数是
- A.120°
- B.112
- C.110°
- D.100°
B
分析：根据轴对称和平行线的性质，可得∠A'DE=∠B，又根据∠C=120°，∠A=26°可求出∠B的值，继而求出答案．
解答：由题意得：∠A'DE=∠B=180°-120°-26°=34°，
∠BDE=180°-∠B=146°，
故∠A'DB=∠BDE-∠A'DE=146°-34°=112°．
故选B．
点评：本题考查了轴对称的性质及三角形中位线定理，有一定难度，根据题意得出各角之间的关系是关键．
分析：根据轴对称和平行线的性质，可得∠A'DE=∠B，又根据∠C=120°，∠A=26°可求出∠B的值，继而求出答案．
解答：由题意得：∠A'DE=∠B=180°-120°-26°=34°，
∠BDE=180°-∠B=146°，
故∠A'DB=∠BDE-∠A'DE=146°-34°=112°．
故选B．
点评：本题考查了轴对称的性质及三角形中位线定理，有一定难度，根据题意得出各角之间的关系是关键．
练习册系列答案
相关题目
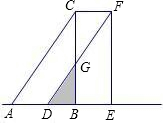如图，将△ABC沿着边AB的方向向右平移2个单位至△DEF，如果AB=4，∠ABC=90°，且△ABC面积为6，则EF=
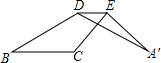（2010•集美区模拟）如图，将△ABC沿着它的中位线DE折叠，点A的对应点为A′，若∠C=120°，∠A=25°，则∠A′DB的度数是
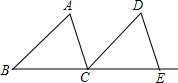如图，将△ABC沿着射线BC的方向平移到△DCE的位置，若BE=14cm，则平移的距离是
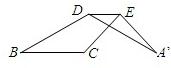15、如图，将△ABC沿着它的中位线DE折迭后，点A落到点A’，若∠C=120°，∠A=26°，则∠A’DB的度数是（ ）