��Ŀ����
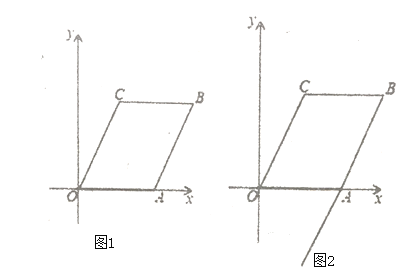
����Ŀ����֪����ͼ1,��ƽ��ֱ������ϵ��,��OΪ����ԭ��,��A��x����������,��C�ڵ�һ����,�ҡ�COA=60��,��OA��OCΪ�ڱ�������OABC,������OABC�����Ϊ![]() .
.
(1)��B. C��������ꣻ
(2)����P��C�����������CB�����˶���ͬʱ����Q��A�����������BA�ķ��������˶���P��Q������˶��ٶȾ�Ϊ2����λ/�룬����PQ��AC��PQ��AC����ֱ�߽��ڵ�D����EΪ�߶�BQ���е㣬����DE���趯��P��Q���˶�ʱ��Ϊt���뽫��DQE�����S�ú�t��ʽ�ӱ�ʾ����ֱ��д��t��ȡֵ��Χ��
(3)��(2)�������£�����Q��QF��y���ڵ�F����tΪ��ֵʱ����P��B.��F.��QΪ������ı���Ϊƽ���ı���?
���𰸡���1����C������Ϊ��(3,3![]() ),��B������Ϊ��(9,3
),��B��������(9,3![]() )����2��S=
)����2��S= ����3����t=0��4sʱ����P.B. F. QΪ������ı���Ϊƽ���ı���.
����3����t=0��4sʱ����P.B. F. QΪ������ı���Ϊƽ���ı���.
��������
��1����ͼ1������C��CD��OA�ڵ�D����ֱ�����������OD��CD�ij����ɽ�����⣮
��2���������������ۼ��ɢ���ͼ2�У���0��t��3ʱ������ͼ3�У���t>3ʱ���ֱ���취�������̼��ɽ�����⣮
��3��������������ͼ4�У���0��t��3ʱ���ڵ�t>3ʱ����PB=QFʱ���۵���Q��y�����ʱ������PB=QF�������̼��ɽ�����⣮
(1)��ͼ1������C��CD��OA�ڵ�D��

������OABC�ı߳�Ϊx����OA=OC=BC=x��
�ߡ�COA=60����
��CD=OCsin60��=![]() x��
x��
������OABC�����Ϊ![]() ��
��
��x![]() x=
x=![]() ��
��
��ã�x=��6��
��OA=OC=BC=6��
��CD=6��![]() =3
=3![]() ,OD=OCcos60��=3��
,OD=OCcos60��=3��
���C��������(3,3![]() ),��B��������(9,3
),��B��������(9,3![]() )��
)��
(2)����ͼ2��,��0t3ʱ,��PK��AB��AC��K������PCK�ǵȱ������Ρ���DH��AB��H.

��PK=PC=AQ����PDK=��ADQ����KPD=��DQA��
���PDK�ա�QDA��
��DK=AD=![]() (62t)=3t,DH=ADsin60��=
(62t)=3t,DH=ADsin60��=![]() (3t),EQ=
(3t),EQ=![]() BQ=
BQ=![]() (6+2t)=3+t��
(6+2t)=3+t��
��S=![]() QEDH=
QEDH=![]() .
.
����ͼ3��,��t>3ʱ,��PK��AB��AC��K�����PCK�ǵȱ������Ρ���DH��AB��H.

�ɡ�PDK�ա�QDA��
��DK=AD=![]() (2t6)=t3,DH=ADsin60��=
(2t6)=t3,DH=ADsin60��=![]() (t3),EQ=
(t3),EQ=![]() BQ=
BQ=![]() (6+2t)=3+t��
(6+2t)=3+t��
��S=![]() QEDH=
QEDH=![]() .
.
��������,S= .
.
(3)����ͼ4�У���0t3ʱ����QK��OA��K.��AK=t��FQ=OK=6t��

��PB=FQʱ���ı���PBQF��ƽ���ı��Σ�
��62t=6t�����t=0.
�ڵ�t>3ʱ����PB=QFʱ��2t6=6t�����t=4��

�۵���Q��y�����ʱ����PB=QF�ɵã�t6=2t6�����t=0���������β�����.
������������t=0��4sʱ����P��B�� F.��QΪ������ı���Ϊƽ���ı���.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij��ѧ��ȤС�����ú�ɫΧ����аڷ�ͼ������Ϸ�У�һͬѧ�ڷ�������ͼ���������ͼ����Ϣ������е�����:
 ������
������
(1)����:
ͼ�α�� | �� | �� | �� | �� | �� |
ͼ�����ӵ����� | ________ | ________ | ________ | �� | �� |
(2)��10��ͼ��������Ϊ________��Χ��;
(3)��ͬѧ��������ڷ���ȥ����ô��![]() ��ͼ��Ҫ��________��Χ��;
��ͼ��Ҫ��________��Χ��;