题目内容
【题目】已知二次函数y=x2﹣2hx+h,当自变量x的取值在﹣1≤x≤1的范围中时,函数有最小值n,则n的最大值是_____.
【答案】![]()
【解析】
根据二次函数的性质可找出二次函数图象的对称轴,分h≤-1、-1<h<1及h≥1三种情况考虑,利用二次函数的性质结合h的取值范围即可找出n的取值范围,取其最大值即可得出结论.
二次函数y=x2-2hx+h图象的对称轴为直线x=h.
当h≤-1时,x=-1时y取最小值,此时n=1+2h+h=1+3h≤-2;
当-1<h<1时,x=h时y取最小值,此时n=h2-2h2+h=-h2+h=-(h-![]() )2+
)2+![]() ≤
≤![]() ;
;
当h≥1时,x=1时y取最小值,此时n=1-2h+h=1-h≤0.
综上所述:n的最大值为![]() .
.
故答案为:![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】某市举行知识大赛,![]() 校、
校、![]() 校各派出
校各派出![]() 名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
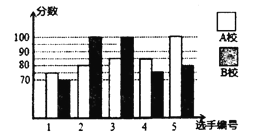
(1)根据图示填写下表:
平均数 | 中位数 | 众数 | |
|
| ||
|
| 80 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.