Question

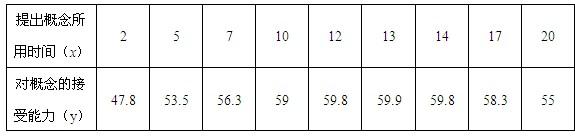
23、心理学家发现，学生对概念的接受能力y与提出概念所用的时间x（单位：分）之间满足函数关系：y=-0.1x²+2.6x+43（0≤x≤30）．y值越大，表示接受能力越强．
（1）x在什么范围内，学生的接受能力逐步增加？x在什么范围内，学生的接受能力逐步降低？
（2）第10分钟时，学生的接受能力是多少？
（3）第几分钟时，学生的接受能力最强？

Answer 1

分析：（1）根据函数关系式求对称轴方程、顶点坐标，结合草图回答问题；
（2）求x=10时y的值；
（3）求函数的最大值．

解答：解：
（1）∵y=-0.1（x²-26x+169）+16.9+43=-0.1（x-13）²+59.9
∴对称轴是：直线x=13
即当（0≤x≤13）提出概念至（13分）之间，学生的接受能力逐步增加；
当（13≤x≤30）提出概念（13分）至3（0分）之间，学生的接受能力逐步降低；
（2）当x=10时，y=-0.1×10²+2.6×10+43=59
（3）当x=13时，y最大59.9即第（13分）钟时，学生的接受能力最强．

点评：此题重在训练二次函数性质的应用，涉及求顶点坐标、对称轴方程、最值问题等，常用配方法结合图象解答问题．