题目内容
【题目】把两个含有45°角的直角三角板如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.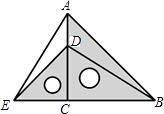
【答案】解:BF⊥AE,理由如下:
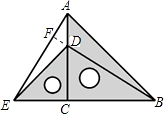
由题意可知:△ECD和△BCA都是等腰Rt△,
∴EC=DC,AC=BC,∠ECD=∠BCA=90°,
在△AEC和△BDC中
EC=DC,∠ECA=∠DCB,AC=BC,
∴△AEC≌△BDC(SAS).
∴∠EAC=∠DBC,AE=BD,
∵∠DBC+∠CDB=90°,∠FDA=∠CDB,
∴∠EAC+∠FDA=90°.
∴∠AFD=90°,即BF⊥AE.
故可得AE⊥BD且AE=BD.
【解析】先观察两条线短的位置关系,当两线段不相交时,可延长构造出三角形,由全等证出对应角相等,转化得到∠EAC+∠FDA=90°,进而证出结果.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目