Question

P为⊙O内与O不重合的一点，则下列说法正确的是（ ）
A．点P到⊙O上任意一点的距离都小于⊙O的半径
B．⊙O上有两点到点P的距离最小
C．⊙O上有两点到点P的距离等于⊙O的半径
D．⊙O上有两点到点P的距离最大

Answer 1

【答案】分析：P为⊙O内与O不重合的一点，则这一点到圆心的距离小于半径，而圆上任意两点之间的距离一定大于0，并且小于或等于直径，则圆内的点到圆上的点的距离一定大于0，且小于直径，因而正确的是C．
解答：解：∵圆内的点到圆上的点的距离一定大于0，且小于直径，
以P为圆心，以⊙O的半径为半径画弧交⊙O于两点M、N，
则M、N到P的距离等于⊙O的半径，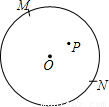
故选C．
点评：本题主要考查了圆内的点与圆上的点之间的距离的大小，可以结合图形进行理解．