题目内容
如图(1)所示,OP是∠MON的平分线,
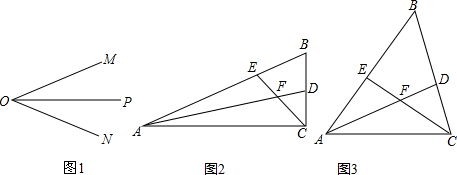
(1)请你利用图(1)画出公共边在角平分线OP上的两个全等三角形并将添加的全等条件标注在图上.
(2)如图(2),在△ABC中,∠ACB=90°,∠B=60°,AD、CE分别是∠BAC,∠BCA的平分线交于F,试判断FE与FD之间的数量关系.
(3)如图(3),在△ABC中,若∠ACB≠90°,而(1)中其他条件不变,请问(1)中所得的结论是否仍然成立?若成立,请证明;若不成立,说明理由.

(1)请你利用图(1)画出公共边在角平分线OP上的两个全等三角形并将添加的全等条件标注在图上.
(2)如图(2),在△ABC中,∠ACB=90°,∠B=60°,AD、CE分别是∠BAC,∠BCA的平分线交于F,试判断FE与FD之间的数量关系.
(3)如图(3),在△ABC中,若∠ACB≠90°,而(1)中其他条件不变,请问(1)中所得的结论是否仍然成立?若成立,请证明;若不成立,说明理由.
分析:(1)只要使OB=OC即可作出全等的三角形;
(2)在AC上截取AG=AE,连接FG,易证△EAF≌△GAF,证得FE=FG,∠EFA=∠GFA=60°,然后证明△FDC≌△FGC,得到FD=FG,从而证明FE=FD;
(3)与(2)的证明类似,首先证明△EAF≌△GAF,证得FE=FG,∠EFA=∠GFA=60°,然后证明△FDC≌△FGC,即可得到.
(2)在AC上截取AG=AE,连接FG,易证△EAF≌△GAF,证得FE=FG,∠EFA=∠GFA=60°,然后证明△FDC≌△FGC,得到FD=FG,从而证明FE=FD;
(3)与(2)的证明类似,首先证明△EAF≌△GAF,证得FE=FG,∠EFA=∠GFA=60°,然后证明△FDC≌△FGC,即可得到.
解答: 解:(1)如以上两图(1)都可以.
解:(1)如以上两图(1)都可以.
(2)如图2,在AC上截取AG=AE,连接FG.
∵AD是∠BAC的平分线,
∴∠EAF=∠GAF,
在△EAF和△GAF中
∴△EAF≌△GAF(SAS),
∴FE=FG,∠EFA=∠GFA=60°.
∴∠GFC=180°-60°-60°=60°.
又∵∠DFC=∠EFA=60°,
∴∠DFC=∠GFC.
在△FDC和△FGC中
∴△FDC≌△FGC(ASA),
∴FD=FG.
∴FE=FD.
(3)结论FE=FD仍成立.
同(2)可得△EAF≌△HAF,
∴FE=FH,∠EFA=∠HFA,
又由(1)可知∠FAC=
∠BAC,∠FCA=
∠ACB,
∴∠FAC+∠FCA=
(∠BAC+∠ACB)=
(180°-∠B)=60°,
∴∠AFC=180°-(∠FAC+∠FCA)=120°,
∴∠EFA=∠HEA=180°-120°=60°,
同(2)可得△FDC≌△FHC,
∴FD=FH,
∴FE=FD.
 解:(1)如以上两图(1)都可以.
解:(1)如以上两图(1)都可以. (2)如图2,在AC上截取AG=AE,连接FG.
∵AD是∠BAC的平分线,
∴∠EAF=∠GAF,
在△EAF和△GAF中
|
∴△EAF≌△GAF(SAS),
∴FE=FG,∠EFA=∠GFA=60°.
∴∠GFC=180°-60°-60°=60°.
又∵∠DFC=∠EFA=60°,
∴∠DFC=∠GFC.
在△FDC和△FGC中
|
∴△FDC≌△FGC(ASA),
∴FD=FG.
∴FE=FD.
(3)结论FE=FD仍成立.
同(2)可得△EAF≌△HAF,
∴FE=FH,∠EFA=∠HFA,
又由(1)可知∠FAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠FAC+∠FCA=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AFC=180°-(∠FAC+∠FCA)=120°,
∴∠EFA=∠HEA=180°-120°=60°,
同(2)可得△FDC≌△FHC,
∴FD=FH,
∴FE=FD.
点评:本题考查了全等三角形的判定与性质,正确构造全等的三角形,理解三个小题之间的联系是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



