题目内容
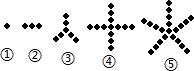 观察图①至⑤中,小黑点的摆放规律,并按这样的规律继续摆放,记第n个图中的小黑点个数为y.解答下列问题:
观察图①至⑤中,小黑点的摆放规律,并按这样的规律继续摆放,记第n个图中的小黑点个数为y.解答下列问题:(1)填表
| n | 1 | 2 | 3 | 4 | 5 | … |
| y | 1 | 3 | … |
(3)当n=50时,小黑点的个数y是多少?
分析:(1)依次数出小黑点的个数即可;
(2)依次得到小黑点的个数与图形序号之间的关系即可;
(3)把n=50代入(2)得到的关系式即可.
(2)依次得到小黑点的个数与图形序号之间的关系即可;
(3)把n=50代入(2)得到的关系式即可.
解答:解:(1)
(2)当n=3时,y=3×2+1=7;
当n=4时,y=4×3+1=13;
…
∴y=n(n-1)+1=n2-n+1
(3)当n=50 时,y=502-50+1=2451.
| n | 1 | 2 | 3 | 4 | 5 | … |
| y | 1 | 3 | 7 | 13 | 21 |
当n=4时,y=4×3+1=13;
…
∴y=n(n-1)+1=n2-n+1
(3)当n=50 时,y=502-50+1=2451.
点评:考查图形的变化规律;得到小黑点的个数与序号n之间的关系是解决本题的关键.

练习册系列答案
相关题目
观察图①至⑤中,小黑点的摆放规律,并按这样的规律继续摆放,记第n个图中的小黑点个数为y. 解答下列问题:
|
n |
1 |
2 |
3 |
4 |
5 |
… |
|
y |
1 |
3 |
|
|
|
… |
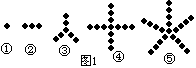
⑴填表
⑵写出求y的公式(用含n的代数式表示)
(3) 当n=50时,小黑点的个数y是多少?
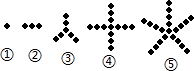 观察图①至⑤中,小黑点的摆放规律,并按这样的规律继续摆放,记第n个图中的小黑点个数为y.解答下列问题:
观察图①至⑤中,小黑点的摆放规律,并按这样的规律继续摆放,记第n个图中的小黑点个数为y.解答下列问题:
(1)填表
| n | 1 | 2 | 3 | 4 | 5 | … |
| y | 1 | 3 | … |
(3)当n=50时,小黑点的个数y是多少?
 观察图1:每个小正方形的边长均是1,我们可以得到小正方形的面积1.
观察图1:每个小正方形的边长均是1,我们可以得到小正方形的面积1. 观察图1:每个小正方形的边长均是1,我们可以得到小正方形的面积1.
观察图1:每个小正方形的边长均是1,我们可以得到小正方形的面积1. 的线段,并说明理由.
的线段,并说明理由.