Question

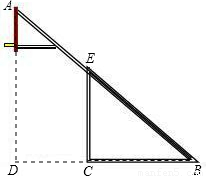
曙光中学需制作一副简易篮球架，如图是篮球架的侧面示意图，已知篮板所在直线AD和直杆EC都与BC垂直，BC=2.8米，CD=1.8米，∠ABD=40°，求斜杆AB与直杆EC的长分别是多少米？（结果精确到0.01米）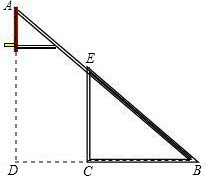

Answer 1

分析：在Rt△BAD中根据已知条件和∠B的三角函数可以求出AB，再在Rt△BEC中根据三角函数就可以求出直杆EC的长．

解答：解：在Rt△BAD中，BD=CD+BC=2.8+1.8=4.6米．
∵cos∠B=

DB

AB

，
∴AB=

DB

cos∠B

=

4.6

cos40°

≈6.00（米）；
在Rt△BEC中，
∵tan∠B=

EC

CB

，
∴EC=CB•tan∠B=2.8×tan40°≈2.35（米）．
则斜杆AB与直杆EC的长分别是2.35米和6.00米．

点评：本题以学校常见的为篮球架背景，考查了学生运用三角函数知识解决实际问题的能力，又让学生感受到生活处处有数学，数学在生产生活中有着广泛的作用．