题目内容
12、从古至今,密码的使用在很多方面都发挥着极其重要的作用.有一种密码的明文(真实文),其中的字母按计算机键盘顺序(自左至右、自上而下)与26个自然数1,2,3,…,25,26对应(见下表).
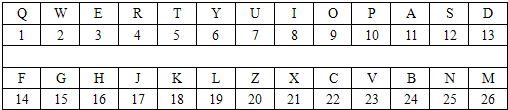
设明文的任一字母对应的自然数为x,译为密文字母后对应的自然数为x'.例如,有一种译码方法按照以下变换实现:x→x',其中x'是(3x+2)被26除所得的余数与1之和(1≤x≤26).
则x=1时,x'=6,即明文Q译为密文Y;x=10时,x'=7,即明文P译为密文U.
现有某变换,将明文字母对应的自然数x变换为密文字母相应的自然数x':x→x',x'为(3x+b)被26除所得余数与1之和(1≤x≤26,1≤b≤26).
已知运用此变换,明文H译为密文T,则明文DAY译成密文为

设明文的任一字母对应的自然数为x,译为密文字母后对应的自然数为x'.例如,有一种译码方法按照以下变换实现:x→x',其中x'是(3x+2)被26除所得的余数与1之和(1≤x≤26).
则x=1时,x'=6,即明文Q译为密文Y;x=10时,x'=7,即明文P译为密文U.
现有某变换,将明文字母对应的自然数x变换为密文字母相应的自然数x':x→x',x'为(3x+b)被26除所得余数与1之和(1≤x≤26,1≤b≤26).
已知运用此变换,明文H译为密文T,则明文DAY译成密文为
CHQ
.分析:根据明文字母对应的自然数x变换为密文字母相应的自然数x':x→x',x'为(3x+b)被26除所得余数与1之和(1≤x≤26,1≤b≤26)推知[(3×13+b)-4]是26的倍数即可得出b的值,易得结果.
解答:解:根据题意,D为13,则(3×13+b)÷26的余数+1=5,
及(3×13+b)÷26的余数为4,
则(3×13+b)-4=26n,
当b=8时,n为整数,
故n=8.
于是关系式可化为x′=(3x+8)÷26的余数+1.
D,A,Y分别对应13,11,6.
则密文号为22,11,1.
故答案为CHQ.
及(3×13+b)÷26的余数为4,
则(3×13+b)-4=26n,
当b=8时,n为整数,
故n=8.
于是关系式可化为x′=(3x+8)÷26的余数+1.
D,A,Y分别对应13,11,6.
则密文号为22,11,1.
故答案为CHQ.
点评:此题以密码知识为载体,考查了同学们的逻辑推理能力,要明确带余除法的意义,可为解题指明方向.

练习册系列答案
相关题目