题目内容
解下列关于x的方程:
(1)(m-1)x2+(2m-1)x+m-3=0;
(2)x2-|x|-1=0;
(3)|x2+4x-5|=6-2x.
解:(1)当m=1时,原方程为:x-2=0,
∴x=2.
当m≠1时,判别式△=(2m-1)2-4(m-1)(m-3)=12m-11,
∴当m≠1且m> 时,x=
时,x= ,
,
当m= 时,△=0,x=
时,△=0,x=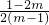 x1=x2=5,
x1=x2=5,
当m< 时,△<0,方程没有实数根.
时,△<0,方程没有实数根.
(2)当x≥0时,原方程为:x2-x-1=0
解方程得:x=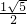 ,
,
∵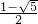 <0,∴x=
<0,∴x=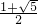 ;
;
当x<0时,原方程为:x2+x-1=0,
解方程得:x=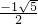 ,
,
∵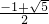 >0,∴x=
>0,∴x=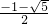 ,
,
故原方程的根为x1=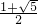 ,x2=-
,x2=-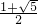 .
.
(3)当x2+4x-5≥0时,原方程为x2+4x-5=6-2x,
整理得:x2+6x-11=0,
解方程得:x= =-3±2
=-3±2 ,
,
当x2+4x-5<0时,原方程为-x2-4x+5=6-2x,
整理得:x2+2x+1=0,
解方程得x1=x2=-1,
故原方程的解为:x1=x2=-1,x3=-3+2 ,x4=-3-2
,x4=-3-2 .
.
分析:(1)若m=1,方程是一元一次,解此一元一次方程;若m≠1,在判别式大于或等于零的情况下,分别求出方程的根,判别式小于零时,方程没有实数根.
(2)由于X带有绝对值符合,必须按X≥0和X<0两种情况解方程,对不合题意的根要舍去.
(3)方程的左边带有绝对值符合,所以按x2+4x-5=6-2x和-x2-4x+=6-2x解方程.
点评:(1)由于方程中含有字母系数,所以在讨论字母系数的范围后,再在不同的范围内求出方程的根;
(2)(3)中都带有绝对值符号,必须分两种情况解方程,对不符合题意的根要舍去.
∴x=2.
当m≠1时,判别式△=(2m-1)2-4(m-1)(m-3)=12m-11,
∴当m≠1且m>
 时,x=
时,x= ,
,当m=
 时,△=0,x=
时,△=0,x=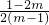 x1=x2=5,
x1=x2=5,当m<
 时,△<0,方程没有实数根.
时,△<0,方程没有实数根.(2)当x≥0时,原方程为:x2-x-1=0
解方程得:x=
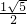 ,
,∵
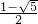 <0,∴x=
<0,∴x=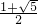 ;
;当x<0时,原方程为:x2+x-1=0,
解方程得:x=
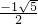 ,
,∵
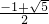 >0,∴x=
>0,∴x=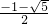 ,
,故原方程的根为x1=
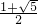 ,x2=-
,x2=-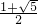 .
.(3)当x2+4x-5≥0时,原方程为x2+4x-5=6-2x,
整理得:x2+6x-11=0,
解方程得:x=
 =-3±2
=-3±2 ,
,当x2+4x-5<0时,原方程为-x2-4x+5=6-2x,
整理得:x2+2x+1=0,
解方程得x1=x2=-1,
故原方程的解为:x1=x2=-1,x3=-3+2
 ,x4=-3-2
,x4=-3-2 .
.分析:(1)若m=1,方程是一元一次,解此一元一次方程;若m≠1,在判别式大于或等于零的情况下,分别求出方程的根,判别式小于零时,方程没有实数根.
(2)由于X带有绝对值符合,必须按X≥0和X<0两种情况解方程,对不合题意的根要舍去.
(3)方程的左边带有绝对值符合,所以按x2+4x-5=6-2x和-x2-4x+=6-2x解方程.
点评:(1)由于方程中含有字母系数,所以在讨论字母系数的范围后,再在不同的范围内求出方程的根;
(2)(3)中都带有绝对值符号,必须分两种情况解方程,对不符合题意的根要舍去.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目