Question

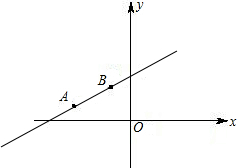已知：直线y=kx+b的图象过点A（-3，1）；B（-1，2），
（1）求：k和b的值；
（2）求：△AOB的面积（O为坐标原点）；
（3）在x轴上有一动点C使得△ABC的周长最小，求C点坐标．

Answer 1

分析：（1）根据待定系数法即可求得k，b的值；
（2）设直线与x轴，y轴交点分别是M，N，在△OMN中，根据三角形的面积即可求得AB边上的高的长度，即可求得三角形的面积；
（3）可以作出A关于x轴的对称点A′，BA′与x轴的交点就是C．

解答：解：（1）根据题意得：

-3k+b=1 -k+b=2

，
解得：

k= 1 2 b= 5 2

；

（2）直线AB的解析式是y=

1

2

x+

5

2

．
设直线与x轴，y轴交点分别是M，N，则M的坐标是（-5，0），N的坐标是（0，

5

2

）．
则MN=

52+( 5 2 )2

=

5 5

2

，设△MNO中，MN边上的高是h．
S_△MNO=

1

2

OM•ON=

1

2

AB•h
解得：h=

5

AB=

(-3+1)2+(2-1)2

=

5

∴△AOB的面积是

1

2

AB•h=

5

2

．

（3）A关于x轴的对称点A′的坐标是（-3，-1）．
设直线A′B的解析式是y=kx+b
根据题意得：

-3k+b=-1 -k+b=2

解得：

k= 3 2 b= 7 2

则直线的解析式是y=

3

2

x+

7

2

在解析式中，令y=0，解得：x=-

7

3

则C的坐标是（-

7

3

，0）．

点评：本题是一次函数与三角形的面积，以及点的对称的综合应用，主要运用了待定系数法，这是一个常用的求解析式的方法．