题目内容
同角三角函数之间的关系：tanA=| sinA |
| cosA |
| cosA |
| sinA |
分析：根据已知条件，tanA=
，cotA=
，直接代入计算即可得tanA•cotA=1；根据三角函数定义可证得sin2A+cos2A=1．
| sinA |
| cosA |
| cosA |
| sinA |
解答：解：（1）∵tanA=
，cotA=
，
∴tanA•cotA=
•
=1；
（2）∵sinA=
，cosA=
，a2+b2=c2，
∴sin2A+cos2A=
+
=
=
=1．
| sinA |
| cosA |
| cosA |
| sinA |
∴tanA•cotA=
| sinα |
| cosα |
| cosα |
| sinα |
（2）∵sinA=
| a |
| c |
| b |
| c |
∴sin2A+cos2A=
| a2 |
| c2 |
| b2 |
| c2 |
| a2+b2 |
| c2 |
| c2 |
| c2 |
点评：本题利用了锐角三角函数的概念和勾股定理对同角的三角函数的关系tanA•cotA=1，sin2A+cos2A=1进行了推导证明．
练习册系列答案
相关题目
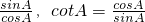，tanA•cotA=________，sin2A+cos2A=________．
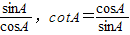，tanA•cotA= ，sin2A+cos2A= ．