题目内容
【题目】设二次函数y=(x-x1)(x-x2) (x1,x2 为实数)
(1)甲求得当x=0时,y=0;当x=1时,y=0;乙求得当x=![]() 时,y=-
时,y=-![]() ,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由。
,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由。
(2)写出二次函数图象的对称轴,并求出该函数的最小值(用含x1,x2的代数式表示)
(3)已知二次函数的图象经过(0,m),和(1,n)两点(m,n是实数),0<x1<x2<1时,求证:0<mn<![]() .
.
【答案】(1)乙求得的结果不正确,理由见解析;(2)-![]() ;(3)见解析
;(3)见解析
【解析】
(1)将(0,0),(1,0)代入y=(x-x1)(x-x2)求出函数解析式即可求解;
(2)对称轴为x=![]() ,当x=
,当x=![]() 时,y=-
时,y=-![]() 函数的最小值;
函数的最小值;
(3)将已知两点代入求出m=x1x2,n=1- x1-x2+x1x2,再表示出mn=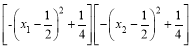 ,由已知0<x1<x2<1,可求出0≤-
,由已知0<x1<x2<1,可求出0≤-![]() ,即可求解.
,即可求解.
(1)当x=0时,y=0;当x=1时,y=0;
∴二次函数经过点(0,0),(1,0),
∴x1=0,x2=1,
∴y═x(x-1)=x![]() -x,
-x,
当x=![]() 时,y=-
时,y=-![]() ,
,
∴乙说点的不对;
(2)对称轴为x=![]() ,当x=
,当x=![]() 时,y=-
时,y=-![]() 是函数的最小值;
是函数的最小值;
(3)二次函数的图象经过(0,m)和(1,n)两点,
∴m=x1x2,n=1- x1-x2+x1x2,,
∴mn=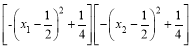
∵0<x1<x2<1,
∴0≤-![]() ,
,![]() ,
,
∴![]() .
.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目