题目内容
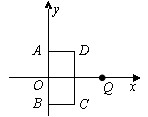
如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
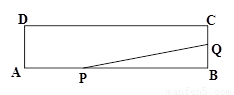
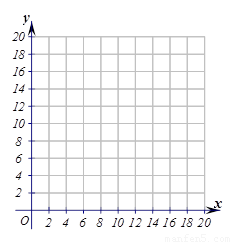
(1)求y关于x的函数关系式,并在右图中画出函数的图像;
(2)求△PBQ面积的最大值.
【答案】
(1)y关于x的函数关系式为:y=-x2+9x(0<x≤4);函数的图像见解析;
(2)△PBQ的最大面积是20cm2.
【解析】
试题分析:(1)借助三角形面积公式求出y关于x的函数关系式,画出函数的图像;
(2)先找到函数的顶点,再由函数单调性和自变量的取值范围求出最大面积。
试题解析:(1)∵S△PBQ= PB·BQ,
PB=AB-AP=18-2x,BQ=x,
PB·BQ,
PB=AB-AP=18-2x,BQ=x,
∴y= (18-2x)x,
(18-2x)x,
即y=-x2+9x(0<x≤4);
函数图像如下图:
 ;
;
(2)由(1)得:y=-x2+9x=-(x- )2 +
)2 + ,
,
∴顶点坐标为( ,
, )
)
∴当0<x≤ 时,y随x的增大而增大,
时,y随x的增大而增大,
∵x的取值范围是0<x≤4,
∴当x=4时,y最大值=20,即△PBQ的最大面积是20cm2.
考点:动点问题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 如图矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E,F,AB=3,BC=4,则图中阴影部分的面积为
如图矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E,F,AB=3,BC=4,则图中阴影部分的面积为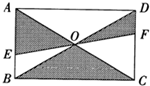 如图矩形ABCD的对角线AC、BD相交于点0,过点0的直线交AB、CD于E、F,AB=6,BC=10,则图中阴影部分的面积为
如图矩形ABCD的对角线AC、BD相交于点0,过点0的直线交AB、CD于E、F,AB=6,BC=10,则图中阴影部分的面积为