题目内容
如图①,将直角边长为1的等腰直角三角形ABC绕其直角顶点C顺时针旋转α角(0°<α<90°),得△A1B1C,A1C交AB于点D,A1B1分别交于BC、AB于点E、F,连接AB1.
(1)求证:△ADC∽△A1DF;
(2)若α=30°,求∠AB1A1的度数;
(3)如图②,当α=45°时,将△A1B1C沿C→A方向平移得△A2B2C2,A2C2交AB于点G,B2C2交BC于点H,设CC2=x(0<x< ),△ABC与△A2B2C2的重叠部分面积为S,试求S与x的函数关系式.
),△ABC与△A2B2C2的重叠部分面积为S,试求S与x的函数关系式.
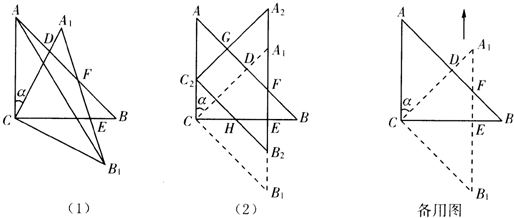
(1)证明:如图,根据旋转变换的性质易知:∠CAD=∠FA1D,
∵∠1=∠2,
∴△ADC∽△A1DF;
(2)解:
(法一)∵CA=CA1=CB=CB1=1,
∵点A、A1、B、B1均在以C为圆心半径为AC的圆上,
∴∠AB1A1=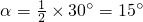 ;
;
(法二)如图①,
∵AC=B1C,
∴∠4=∠3,
∵α=30°,∠A1CB1=90°,
∴∠ACB1=120°,
∴∠4=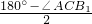 =30°,
=30°,
∴∠AB1A1=∠CB1A1-∠4=45°-30°=15°;
(法三)如图①,
∵AC=B1C,
∴∠4=∠3,
∵∠CAB=∠CB1A1,
∴∠CAB-∠3=∠CB1A1-∠4,
即∠B1AB=∠AB1A1,
∵∠5=∠B1AB+∠AB1A1,
∴∠5=2∠AB1A1,
∵△ADC∽△A1DF,
∴∠5=α,
∴∠AB1A1= ;
;
(3)解:△A1B1C在平移的过程中,易证得△AC2G、△HB2E、△A2FG、△C2HC、△FBE均是等腰直角三角形,四边形AC2B2F是平行四边形,
∵AB=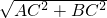 =
= ,
,
∴当α=45°时,CE=CD= AB=
AB= ,
,
情形①:当0<x<1时(如图2所示),
△A2B2C2与△ABC的重叠部分为五边形C2HEFG,
S五边形C2HEFG=S平行四边形AC2B2F-SRt△AC2G-SRt△HB2E,
∵C2C=x,
∴CH=x,AC2=1-x,B2E=HE=1-x,
∴AG=C2G= AC2=
AC2= (1-x)=
(1-x)= -
- x,
x,
∴S平行四边形AC2B2F=AC2•CE=( -
- x)•
x)• =
= -
- x,
x,
SRt△AC2G= •AG2=
•AG2= (
( -
- x) 2=
x) 2= x2-
x2- x+
x+ ,
,
SRt△HB2E= •B2E2=
•B2E2=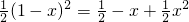 ,
,
∴S五边形C2HEFG= -
- x-(
x-( x2-
x2- x+
x+ )-(
)-(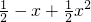 )=-
)=- x2+x-
x2+x- ,
,
情形②:当1≤x< 时(如图3所示),
时(如图3所示),
△A2B2C2与△ABC的重叠部分为直角梯形C2B2FG,
S直角梯形C2B2FG=S平行四边形C2B2FA-SRt△AC2G=AC2•CE- AG2
AG2
= -
- x-(
x-( x2-
x2- x+
x+ )=-
)=- x2+
x2+ ;
;
分析:(1)根据旋转变换的性质得到:∠CAD=∠FA1D,又由∠1=∠2,易证得△ADC∽△A1DF;
(2)由四点共圆的知识,易得点A、A1、B、B1均在以C为圆心半径为的圆上,又由同弧所对的圆周角相等,可求得∠AB1A1的度数;
(3)△A1B1C在平移的过程中,易证得△AC2G、△HB2E、△A2FG、△C2HC、△FBE均是等腰直角三角形,四边形AC2B2F是平行四边形,然后由勾股定理即可求得S与x的函数关系式.
点评:此题考查了相似三角形的判定与性质,以及平移的性质与平行四边形的性质.题目比较复杂,特别是图形复杂,解题时要注意仔细识图,准确的应用数形结合思想.
∵∠1=∠2,
∴△ADC∽△A1DF;
(2)解:
(法一)∵CA=CA1=CB=CB1=1,
∵点A、A1、B、B1均在以C为圆心半径为AC的圆上,
∴∠AB1A1=
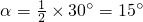 ;
;(法二)如图①,

∵AC=B1C,
∴∠4=∠3,
∵α=30°,∠A1CB1=90°,
∴∠ACB1=120°,
∴∠4=
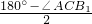 =30°,
=30°,∴∠AB1A1=∠CB1A1-∠4=45°-30°=15°;
(法三)如图①,
∵AC=B1C,
∴∠4=∠3,
∵∠CAB=∠CB1A1,
∴∠CAB-∠3=∠CB1A1-∠4,
即∠B1AB=∠AB1A1,
∵∠5=∠B1AB+∠AB1A1,
∴∠5=2∠AB1A1,
∵△ADC∽△A1DF,
∴∠5=α,
∴∠AB1A1=
 ;
;(3)解:△A1B1C在平移的过程中,易证得△AC2G、△HB2E、△A2FG、△C2HC、△FBE均是等腰直角三角形,四边形AC2B2F是平行四边形,

∵AB=
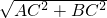 =
= ,
,∴当α=45°时,CE=CD=
 AB=
AB= ,
,情形①:当0<x<1时(如图2所示),
△A2B2C2与△ABC的重叠部分为五边形C2HEFG,
S五边形C2HEFG=S平行四边形AC2B2F-SRt△AC2G-SRt△HB2E,
∵C2C=x,
∴CH=x,AC2=1-x,B2E=HE=1-x,
∴AG=C2G=
 AC2=
AC2= (1-x)=
(1-x)= -
- x,
x,∴S平行四边形AC2B2F=AC2•CE=(
 -
- x)•
x)• =
= -
- x,
x,
SRt△AC2G=
 •AG2=
•AG2= (
( -
- x) 2=
x) 2= x2-
x2- x+
x+ ,
,SRt△HB2E=
 •B2E2=
•B2E2=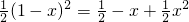 ,
,∴S五边形C2HEFG=
 -
- x-(
x-( x2-
x2- x+
x+ )-(
)-(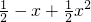 )=-
)=- x2+x-
x2+x- ,
,情形②:当1≤x<
 时(如图3所示),
时(如图3所示),△A2B2C2与△ABC的重叠部分为直角梯形C2B2FG,
S直角梯形C2B2FG=S平行四边形C2B2FA-SRt△AC2G=AC2•CE-
 AG2
AG2=
 -
- x-(
x-( x2-
x2- x+
x+ )=-
)=- x2+
x2+ ;
;分析:(1)根据旋转变换的性质得到:∠CAD=∠FA1D,又由∠1=∠2,易证得△ADC∽△A1DF;
(2)由四点共圆的知识,易得点A、A1、B、B1均在以C为圆心半径为的圆上,又由同弧所对的圆周角相等,可求得∠AB1A1的度数;
(3)△A1B1C在平移的过程中,易证得△AC2G、△HB2E、△A2FG、△C2HC、△FBE均是等腰直角三角形,四边形AC2B2F是平行四边形,然后由勾股定理即可求得S与x的函数关系式.
点评:此题考查了相似三角形的判定与性质,以及平移的性质与平行四边形的性质.题目比较复杂,特别是图形复杂,解题时要注意仔细识图,准确的应用数形结合思想.

练习册系列答案
相关题目


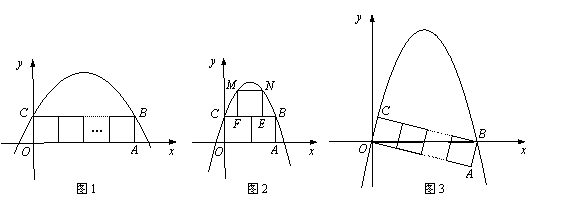
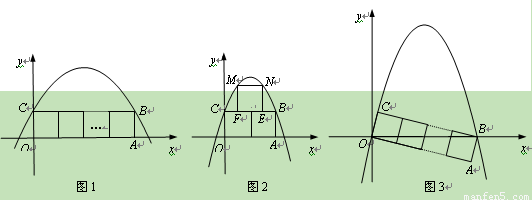
 个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在
个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在 轴和
轴和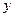 轴的正半轴上, 设抛物
轴的正半轴上, 设抛物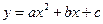
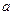 <0)过矩形顶点B、C.
<0)过矩形顶点B、C.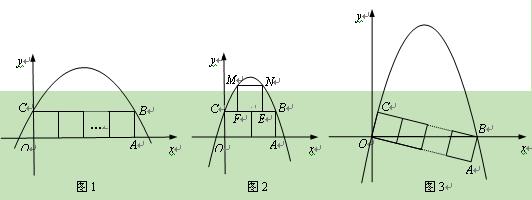
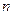 个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在
个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在 轴和
轴和 轴的正半轴上, 设抛物
轴的正半轴上, 设抛物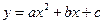
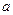 <0)过矩形顶点B、C.
<0)过矩形顶点B、C.
 个边长为1的正方形并排组成矩形OABC, 相邻两边OA和OC分别落在
个边长为1的正方形并排组成矩形OABC, 相邻两边OA和OC分别落在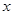 轴和
轴和 轴的正半轴上, 设抛物
轴的正半轴上, 设抛物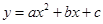
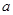 <0)过矩形顶点B、C.
<0)过矩形顶点B、C.