题目内容
在⊙O中,弦AB∥CD,且⊙O的半径r=10,AB=12,CD=16,则两弦间的距离
14或2
14或2
.分析:过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,由题意可得:OA=OC=10,AF=FB=6,CE=ED=8,E、F、O在一条直线上,EF为AB、CD之间的距离,再分别解Rt△OEC、Rt△OFA,即可得OE、OF的长,然后分AB、CD在圆心的同侧和异侧两种情况求得AB与CD的距离.
解答: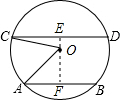 解:①当AB、CD在圆心两侧时;
解:①当AB、CD在圆心两侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图所示:
∵半径r=10,弦AB∥CD,且AB=12,CD=16,
∴OA=OC=10,AF=FB=6,CE=ED=8,E、F、O在一条直线上,
∴EF为AB、CD之间的距离,
在Rt△OEC中,由勾股定理可得:OE2=OC2-CE2,
∴OE=
=6,
在Rt△OFA中,由勾股定理可得:OF2=AO2-AF2,
∴OF=
=8,
∴EF=OE+OF=6+8=14,即AB与CD的距离为14;
②当AB、CD在圆心同侧时;
同①可得:OE=6,OF=8;
则AB与CD的距离为:OF-OE=2,
综上,两弦间的距离为14或2.
故答案为:14或2
 解:①当AB、CD在圆心两侧时;
解:①当AB、CD在圆心两侧时;过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图所示:
∵半径r=10,弦AB∥CD,且AB=12,CD=16,
∴OA=OC=10,AF=FB=6,CE=ED=8,E、F、O在一条直线上,
∴EF为AB、CD之间的距离,
在Rt△OEC中,由勾股定理可得:OE2=OC2-CE2,
∴OE=
| 102-82 |
在Rt△OFA中,由勾股定理可得:OF2=AO2-AF2,
∴OF=
| 102-62 |
∴EF=OE+OF=6+8=14,即AB与CD的距离为14;
②当AB、CD在圆心同侧时;
同①可得:OE=6,OF=8;
则AB与CD的距离为:OF-OE=2,
综上,两弦间的距离为14或2.
故答案为:14或2
点评:此题考查了垂径定理,以及勾股定理,利用了分类讨论的思想,熟练掌握垂径定理是解本题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
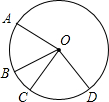 如图,在⊙O中,弦AB=CD,图中的线段、角、弧分别具有相等关系的量共有(不包括AB=CD)( )
如图,在⊙O中,弦AB=CD,图中的线段、角、弧分别具有相等关系的量共有(不包括AB=CD)( )| A、10组 | B、7组 | C、6组 | D、5组 |
 如图,在⊙O中,弦AB⊥弦CD于E,弦AG⊥弦BC于F点,连EF,CD与AG相交于M点,则下列结论:①BD=BG;②DE=EM;③∠ACD=∠AFE;④AF=BF,其中正确的有
如图,在⊙O中,弦AB⊥弦CD于E,弦AG⊥弦BC于F点,连EF,CD与AG相交于M点,则下列结论:①BD=BG;②DE=EM;③∠ACD=∠AFE;④AF=BF,其中正确的有 如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.
如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD. 如图,在⊙O中,弦AB=3.6cm,圆周角∠ACB=30°,则⊙O的直径等于( )
如图,在⊙O中,弦AB=3.6cm,圆周角∠ACB=30°,则⊙O的直径等于( )