题目内容
【题目】如图，将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形，这个黑色菱形可分割成n个边长为1的小三角形，若 
= 
，则△ABC的边长是 ． 
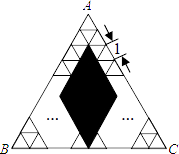
【答案】12
【解析】解：设正△ABC的边长为x，则高为 
x， S△ABC= 
x x= 
x2 ，
∵所分成的都是正三角形，
∴结合图形可得黑色菱形的较长的对角线为 x﹣ 
，较短的对角线为（ x﹣ ） = x﹣1，
∴黑色菱形的面积= （ x﹣ ）（ x﹣1）= 
（x﹣2）2 ，
∴ 
= 
= 
，
整理得，11x2﹣144x+144=0，
解得x1= 
（不符合题意，舍去），x2=12，
所以，△ABC的边长是12．
所以答案是：12．
【考点精析】认真审题，首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°)，还要掌握菱形的性质(菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半)的相关知识才是答题的关键．
【题目】为了解某品牌A，B两种型号冰箱的销售情况，王明对某专卖店一到七月份的销售情况进行了统计，并将得到的数据制成如下统计表：
月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
A型销 售量(台) | 10 | 14 | 17 | 16 | 13 | 14 | 14 |
B型销 售量(台) | 6 | 10 | 14 | 15 | 16 | 17 | 20 |
完成下表：
平均数(台) | 中位数(台) | 方差 | |
A型销售量 | 14 | ||
B型销售量 | 14 | 18.6 |
【题目】问题背景：
小红同学在学习过程中遇到这样一道计算题“计算4×3.142﹣4×3.14×3.28+3.282”，他觉得太麻烦，估计应该有可以简化计算的方法，就去请教崔老师．崔老师说：你完成下面的问题后就可能知道该如何简化计算啦！
获取新知：
请你和小红一起完成崔老师提供的问题：
（1）填写下表：
x=﹣1，y=1 | x=1，y=0 | x=3，y=2 | x=1，y=1 | x=5，y=3 | |
A=2x﹣y | ﹣3 | 2 | 4 | 1 | 7 |
B=4x2﹣4xy+y2 | 9 | 4 |
|
|
|
（2）观察表格，你发现A与B有什么关系？
解决问题：
（3）请结合上述的有关信息，计算4×3.142﹣4×3.14×3.28+3.282．
