题目内容

精英家教网在反比例函数y=
1x
（x＞0）的图象上，有一系列点P1、P2、P3、…、Pn，若P1的横坐标为2，且以后每点的横坐标与它前一个点的横坐标的差都为2．现分别过点P1、P2、P3、…、Pn作x轴与y轴的垂线段，构成若干个长方形如图所示，将图中阴影部分的面积从左到右依次记为S1、S2、S3、…、Sn，则S1+S2+S3+…+S2010=
 
．
分析：易求得P1的坐标得到矩形P1AOB的面积；而把所有的阴影部分平移到左边，阴影部分的面积之和就等于矩形P1AOB的面积，即可得到答案．
解答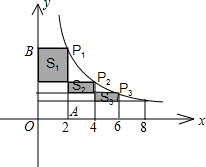：精英家教网解：如图，过点P1、点P2010作y轴的垂线段，垂足分别是点B、点C，过点P1作x轴的垂线段，垂足是点E，P1E交CP2010于点A，
则点A的纵坐标等于点P2010的纵坐标等于
1
2×2010
，AC=2，AE=
1
2×2010
，
故S1+S2+S3+…+S2010=S矩形P1EOCB-S矩形AEOC=2×
1
2
-2×
1
2×2011
=
2010
2011
．
故答案为
2010
2011
．
点评：本题考查了点在反比例函数图象上，则点的横纵坐标满足其解析式．也考查了图形的平移以及矩形的性质．
练习册系列答案
相关题目
已知：点A（m，m）在反比例函数y=
1x
的图象上，点B与点A关于坐标轴对称，以AB为边作等边△ABC，则满足条件的点C有
 
个．
点P（2m-3，1）在反比例函数y=
1x
的图象上，则m=
 
．
若点（-2，y1）、（-1，y2）在反比例函数y=
1
x
的图象上，则下列结论中正确的是（　　）
A、y1＞y2
B、y2＞y1
C、y2=y1
D、无法确定
已知点（-1，a），（1，b），（3，c）均在反比例函数y=-
1
x
的图象上，则（　　）
A、a＞b＞c
B、c＞b＞a
C、a＞c＞b
D、b＞c＞a
若点（-2，y1）、（-1，y2）、（1，y3）都在反比例函数y=-
1x
的图象上，则用“＞”连接y1、y2、y3得
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网