Question

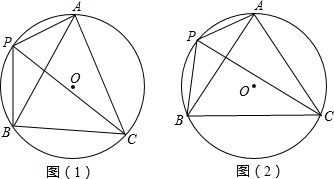
（2013•武汉）如图，已知△ABC是⊙O的内接三角形，AB=AC，点P是

AB

的中点，连接PA，PB，PC．
（1）如图①，若∠BPC=60°．求证：AC=

3

AP；
（2）如图②，若sin∠BPC=

24

25

，求tan∠PAB的值．

Answer 1

分析：（1）根据圆周角定理得∠BPC=∠BAC=60°，可判断△ABC为等边三角形，∠ACB=∠ABC=60°，再利用圆周角定理得到∠APC=∠ABC=60°，而点P是

AB

的中点，则∠ACP=

1

2

∠ACB=30°，于是∠PAC=90°，然后根据30度的正切可计算出AC=

3

AP；
（2）过A点作AD⊥BC交BC于D，连结OP交AB于E，根据垂径的推论得到点O在AD上，连结OB，根据圆周角定理得∠BOD=∠BAC，∠BPC=∠BAC，所以sin∠BOD=sin∠BPC=

24

25

=

BD

OB

，设OB=25x，则BD=24x，在Rt△OBD中可计算出OD=7x，再在Rt△ABD计算出AB=40x，由于点P是

AB

的中点，根据垂径定理的推论OP垂直平分AB，则AE=

1

2

AB=20x，
在Rt△AEO中，根据勾股定理计算出OE=15x，所以PE=OP-OE=25x-15x=10x，最后在Rt△APE中，利用正切的定义求解．

解答：解：（1）∵∠BPC=60°，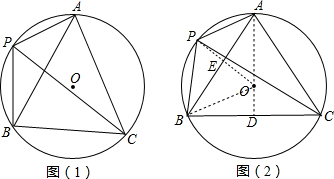
∴∠BAC=60°，
∵AB=AC，
∴△ABC为等边三角形，
∴∠ACB=∠ABC=60°，
∴∠APC=∠ABC=60°，
而点P是

AB

的中点，
∴∠ACP=

1

2

∠ACB=30°，
∴∠PAC=90°，
∴tan∠PCA=

PA

AC

=tan30°=

3

3

，
∴AC=

3

PA；

（2）过A点作AD⊥BC交BC于D，连结OP交AB于E，如图，
∵AB=AC，
∴AD平分BC，
∴点O在AD上，
连结OB，则∠BOD=∠BAC，
∵∠BPC=∠BAC，
∴sin∠BOD=sin∠BPC=

24

25

=

BD

OB

，
设OB=25x，则BD=24x，
∴OD=

OB2-BD2

=7x，
在Rt△ABD中，AD=25x+7x=32x，BD=24x，
∴AB=

AD2+BD2

=40x，
∵点P是

AB

的中点，
∴OP垂直平分AB，
∴AE=

1

2

AB=20x，∠AEP=∠AEO=90°，
在Rt△AEO中，OE=

AO2-AE2

=15x，
∴PE=OP-OE=25x-15x=10x，
在Rt△APE中，tan∠PAE=

PE

AE

=

10x

20x

=

1

2

，
即tan∠PAB的值为

1

2

．

点评：本题考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧．也考查了勾股定理、圆周角定理和解直角三角形．