Question

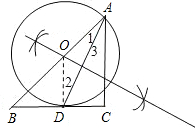
如图，在Rt△ABC中，∠C=90°，AD是∠BAC的角平分线，以AB上一点O为圆心，AD为弦作⊙O．
（1）在图中作出⊙O（不写作法，保留作图痕迹）；
（2）求证：BC为⊙O的切线；
（3）若AC=3，tanB=

3

4

，求⊙O的半径长．

Answer 1

（1）如图，（2分）

（2）证明：连接OD．
∵OA=OD，
∴∠1=∠2，
∵∠1=∠3，
∴∠2=∠3，
∴OD∥AC．（3分）
又∵∠C=90°，∴∠ODB=90°，（5分）
∴BC是⊙O的切线；（6分）

（3）在Rt△ABC中，AC=3，tanB=

3

4

．
∴BC=4，
∴AB=

32+42

=5，（7分）
∵OD∥AC，
∴△OBD∽△ABC，（8分）
所以

OB

AB

=

OD

AC

，

5-OA

5

=

OA

3

，
∴OA=OD=

15

8

，
∴⊙的半径为

15

8

．