题目内容
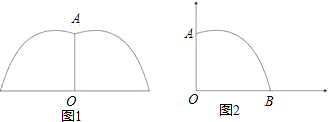
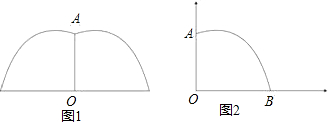
某公园要建造一个圆形的喷水池，在水池中央垂直于水面竖一根柱子，上面的A处安装一个喷头向外喷水，连喷头在内，柱高为0.8m，如图建立直角坐标系，水流喷出的高度y（m）与水面距离x（m）之间的函
数关系式为y=-x2+2x+| 4 | 5 |
（1）求喷出的水流距水平面的最大高度
（2）水池的半径至少为
分析：已知函数关系式求最值可运用配方法或公式法；求水池半径即求图中OB的长，当y=0时x的值即是．
解答：解：（1）∵y=-（x-1）2+
，
∴当x=1时，y有最大值
，
∴最大高度为
m．
（2）令y=0，则-（x-1）2+
=0，
∴x=1±
，
又∵x＞0，
∴x=1+
，
∴B（1+
，0），
∴OB=1+
．
∴水池半径至少为（1+
）m．
| 9 |
| 5 |
∴当x=1时，y有最大值
| 9 |
| 5 |
∴最大高度为
| 9 |
| 5 |
（2）令y=0，则-（x-1）2+
| 9 |
| 5 |
∴x=1±
3
| ||
| 5 |
又∵x＞0，
∴x=1+
| 3 |
| 5 |
| 5 |
∴B（1+
3
| ||
| 5 |
∴OB=1+
3
| ||
| 5 |
∴水池半径至少为（1+
3
| ||
| 5 |
点评：已知二次函数的表达式求最值问题常配成顶点式形式，亦可运用公式求解．
练习册系列答案
相关题目
．
．
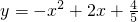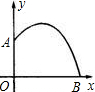数关系式为y=-x2+2x+
．