Question

（1997•昆明）甲、乙两人分别从相距18公里的A、B两地同时相向而行，甲以4公里/小时的平均速度步行，乙以每小时比甲快1公里的平均速度步行，相遇而止．
（1）求甲、乙二人相距的距离y（公里）和所用的时间x（小时）的函数关系式；
（2）求出函数图象与x轴、y轴的交点坐标，画出函数的图象，并求出自变量x的取值范围；
（3）求当甲、乙二人相距6公里时，所需用的时间．

Answer 1

分析：（1）根据两人的速度得出，两人行驶距离之和+y=18，即可得出函数关系式；
（2）根据（1）中所求得出图象与x轴、y轴的交点坐标以及自变量的取值范围，画出函数的图象，即可得出；
（3）根据已知得出当y=6时，求出x的值即可．

解答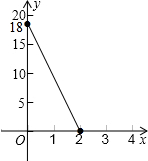：解：（1）∵甲以4公里/小时的平均速度步行，乙以每小时比甲快1公里的平均速度步行，
∴乙以5公里/小时的平均速度步行，
∵甲、乙两人分别从相距18公里的A、B两地同时相向而行，
∴甲、乙二人相距的距离y（公里）和所用的时间x（小时）的函数关系式：
y=18-（4+5）x=18-9x；

（2）当x=0，则y=18，故图象与y轴交点坐标为：（0，18），
当y=0，则x=2，故图象与x轴交点坐标为：（2，0），
∵0≤y≤18，
∴自变量x的取值范围为：0≤x≤2；

（3）∵A、B两地同时相向而行，相遇而止，当甲、乙二人相距6公里时，即y=6，
则6=18-9x，
解得：x=

4

3

，
答：当甲、乙二人相距6公里时，所需用的时间为

4

3

小时．

点评：此题主要考查了一次函数的应用以及一次函数与坐标轴交点求法和图象画法，利用数形结合得出图象自变量取值范围是解题关键．