题目内容
(2007•牡丹江)如图,在平面直角坐标系中,已知点A(-3,6),点B,点C分别在x轴的负半轴和正半轴上,OB,OC的长分别是方程x2-4x+3=0的两根(OB<OC).(1)求B,C两点的坐标;
(2)在坐标平面内是否存在点Q和点P(点P在直线AC上),使以O、P、C、Q为顶点的四边形是正方形?若存在,请直接写出Q点的坐标;若不存在,请说明理由;
(3)若平面内有M(1,-2),D为线段OC上一点,且满足∠DMC=∠BAC,∠MCD=45°,求直线AD的解析式.

【答案】分析:(1)解方程x2-4x+3=0就可以求出x的值,即B,C的横坐标,就可以得到B,C的坐标.
(2)以O、P、C、Q为顶点的四边形是正方形,O、C的坐标已知,就可以写出Q的坐标.
(3)过A作AH⊥x轴于H点,可以证出△CAB∽△CMD,得到 ,
,
在直角△AHC中,根据勾股定理得出AC,就可以求出OD的长.
根据待定系数法就可以求出函数解析式.
解答:解:(1)x2-4x+3=0,得x=3或1,
∵OB<OC,
∴B(-1,0),C(3,0);
(2)存在.
Q1(3,3)或 ;
;
(3)过A作AH⊥x轴于H点.
则AH=CH=6,∴∠ACB=45°,
同理可证:∠DCM=45°,
∴∠ACB=∠DCM.
又∵∠DMC=∠BAC,
∴△CAB∽△CMD,
∴ (1分)
(1分)
在△AHC中, ,
,
同理 ,(1分)
,(1分)
∴ ,
,
∴ ,
,
∴ ,
, . (1分)
. (1分)
设AD的解析式为y=kx+b(k≠0),则 ,
,
∴ ,
,
∴y=- x+
x+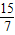 .
.
点评:本题主要考查了待定系数法求函数解析式.运用了相似三角形的对应边的比相等,就可以求出.
(2)以O、P、C、Q为顶点的四边形是正方形,O、C的坐标已知,就可以写出Q的坐标.
(3)过A作AH⊥x轴于H点,可以证出△CAB∽△CMD,得到
 ,
,在直角△AHC中,根据勾股定理得出AC,就可以求出OD的长.
根据待定系数法就可以求出函数解析式.
解答:解:(1)x2-4x+3=0,得x=3或1,
∵OB<OC,
∴B(-1,0),C(3,0);
(2)存在.
Q1(3,3)或
 ;
;(3)过A作AH⊥x轴于H点.

则AH=CH=6,∴∠ACB=45°,
同理可证:∠DCM=45°,
∴∠ACB=∠DCM.
又∵∠DMC=∠BAC,
∴△CAB∽△CMD,
∴
 (1分)
(1分)在△AHC中,
 ,
,同理
 ,(1分)
,(1分)∴
 ,
,∴
 ,
,∴
 ,
, . (1分)
. (1分)设AD的解析式为y=kx+b(k≠0),则
 ,
,∴
 ,
,∴y=-
 x+
x+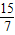 .
.点评:本题主要考查了待定系数法求函数解析式.运用了相似三角形的对应边的比相等,就可以求出.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
