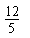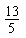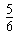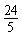题目内容
在同一平面上把三边BC=3,AC=4,AB=5的三角形沿最长边AB翻折后得到△ABC′,则CC′的长等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据勾股定理的逆定理,知该三角形是直角三角形.根据翻折前后的图形全等,知CC′的长为直角三角形ABC高的2倍.
解答:解:如图所示,
连接CC′,根据对称的性质可知CC′⊥AB,且CC′=2CE,
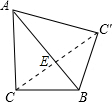
∵
AC×BC=
AB×CE,
∴CE=
,
∴CC′=2×CE=
.
故选:D.
连接CC′,根据对称的性质可知CC′⊥AB,且CC′=2CE,

∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CE=
| 12 |
| 5 |
∴CC′=2×CE=
| 24 |
| 5 |
故选:D.
点评:本题考查的是图形翻折变换的性质,根据题意画出图形是解答此题的关键.注意:根据三角形的面积公式可以导出直角三角形斜边上的高等于两条直角边的积除以斜边.

练习册系列答案
相关题目
在同一平面上把三边BC=3,AC=4,AB=5的三角形沿最长边翻折成△ABC′,则CC′等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|