题目内容
瑞士一位中学教师巴尔末从光谱数据
,
,
,
…中发现了一个规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据光谱数据的前四个数写出第n个数,为
或
或
.
| 9 |
| 5 |
| 16 |
| 12 |
| 25 |
| 21 |
| 36 |
| 32 |
| (n+2)2 |
| n(n+4) |
| (n+2)2 |
| (n+2)2-4 |
| (n+2)2 |
| n(n+4) |
| (n+2)2 |
| (n+2)2-4 |
分析:根据
=
,
=
,
=
,
=
得出分子与分母的变化,进而得出规律即可.
| 9 |
| 5 |
| (1+2)2 |
| 1×(1+4) |
| 16 |
| 12 |
| (2+2)2 |
| 2×(2+4) |
| 25 |
| 21 |
| (3+2)2 |
| 3×(3+4) |
| 36 |
| 32 |
| (4+2)2 |
| 4×(4+4) |
解答:解:∵
=
,
=
,
=
,
=
…
∴第n个数为:
,
故答案为:
.
| 9 |
| 5 |
| (1+2)2 |
| 1×(1+4) |
| 16 |
| 12 |
| (2+2)2 |
| 2×(2+4) |
| 25 |
| 21 |
| (3+2)2 |
| 3×(3+4) |
| 36 |
| 32 |
| (4+2)2 |
| 4×(4+4) |
∴第n个数为:
| (n+2)2 |
| n(n+4) |
故答案为:
| (n+2)2 |
| n(n+4) |
点评:此题主要考查了数字变化规律,根据数字中分子与分母的变化规律是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
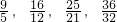 …中发现了一个规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据光谱数据的前四个数写出第n个数,为________.
…中发现了一个规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据光谱数据的前四个数写出第n个数,为________.