Question

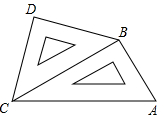小明将一幅三角板如图所示摆放在一起，发现只要知道其中一边的长就可以求出其它各边的长，若已知CD=2，求AC的长．

Answer 1

分析：在直角△BDC中根据勾股定理得到BC的长，进而在直角△ABC中，根据勾股定理，求出AC的长．

解答：解：∵BD=CD=2，
∴BC=

22+22

=2

2

，
∴设AB=x，则AC=2x，
∴x2+(2

2

)2=(2x)2，
∴x²+8=4x²，
∴3x²=8，
∴x²=

8

3

，
∴x=

2 6

3

，
AC=2AB=

4

3

6

．

点评：本题解决的关键是利用勾股定理，先求出两个直角三角形的公共边BC．