Question

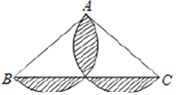
【题目】如图，在△ABC中，AB=AC，AB=8，BC=12，分别以AB、AC为直径作半圆，则图中阴影部分的面积是为________________.

Answer 1

【答案】

【解析】设半圆与底边的交点是D，连接AD．根据直径所对的圆周角是直角，得到AD⊥BC，再根据等腰三角形的三线合一，得到BD=CD=6，根据勾股定理即可求得AD的长，则阴影部分的面积是以AB为直径的圆的面积减去三角形ABC的面积．

解：设半圆与底边的交点是D，连接AD．

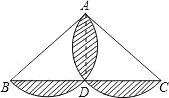
∵AB是直径，∴AD⊥BC．
又∵AB=AC，∴BD=CD=6．
根据勾股定理，得
AD==2．
∵阴影部分的面积的一半=以AB为直径的半圆的面积-三角形ABD的面积
=以AC为直径的半圆的面积-三角形ACD的面积，
∴阴影部分的面积=以AB为直径的圆的面积-三角形ABC的面积

=16π×12×2=16π-12．
故答案为：16π-12．

“点睛”此题综合运用了圆周角定理的推论、等腰三角形的三线合一、勾股定理、圆面积公式和三角形的面积公式．