题目内容
已知x、y为正数，且|x2-4|+（y2-3）2=0，如果以x、y的长为直角边作一个直角三角形，那么以这个直角三角形的斜边为边长的正方形的面积为（ ）
| A、5 | B、25 | C、7 | D、15 |
分析：本题可根据“两个非负数相加和为0，则这两个非负数的值均为0”解出x、y的值，然后运用勾股定理求出斜边的长．斜边长的平方即为正方形的面积．
解答：解：依题意得：x2-4=0，y2-3=0，
∴x=2，y=
，
斜边长=
=
，
所以正方形的面积=（
）2=7．
故选C．
∴x=2，y=
| 3 |
斜边长=
| 4+3 |
| 7 |
所以正方形的面积=（
| 7 |
故选C．
点评：本题综合考查了勾股定理与非负数，解这类题的关键是利用直角三角形，用勾股定理来寻求未知系数的等量关系．
练习册系列答案
相关题目
已知
，
，
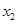均为正数，且满足
，
，则M与N之间的关系是（ ）
| A．M＞N | B．M＝N | C．M＜N | D．无法确定 |
，
，
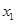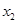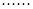
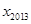均为正数，且满足
，
，则M与N之间的关系是（ ）