题目内容
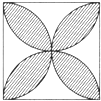如图所示，正方形的边长为a，以各边为直径在正方形内画半圆，则所围成图形（阴影部分）的面积为| 1 |
| 2 |
| 1 |
| 2 |
分析：设出每部分的面积，分别求出阴影部分的面积、4个半圆的面积、正方形的面积是S正方形推出S阴影=4个半圆的面积-正方形的面积，根据圆的面积和三角形的面积求出即可．
解答：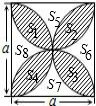
解：如图，∵S阴影=S1+S2+S3+S4，
4个半圆的面积是（S1+S2+S5）+（S2+S6+S3）+（S3+S7+S4）+（S1+S8+S4）=（S1+S2+S3+S4）+（S1+S2+S3+S4+S5+S6+S7+S8），
正方形的面积是S正方形=S1+S2+S3+S4+S5+S6+S7+S8，
∴S阴影=4个半圆的面积-正方形的面积，
=2×π×（
）2-a2
=
π a2-a2．
故答案为：
π a2-a2．
解：如图，∵S阴影=S1+S2+S3+S4，4个半圆的面积是（S1+S2+S5）+（S2+S6+S3）+（S3+S7+S4）+（S1+S8+S4）=（S1+S2+S3+S4）+（S1+S2+S3+S4+S5+S6+S7+S8），
正方形的面积是S正方形=S1+S2+S3+S4+S5+S6+S7+S8，
∴S阴影=4个半圆的面积-正方形的面积，
=2×π×（
| a |
| 2 |
=
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查列代数式，找到阴影部分的面积的等量关系是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
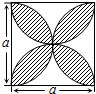如图所示，正方形的边长为a，以各边为直径在正方形内画半圆，则阴影部分的面积为（ ）| A、2πa2-2a2 | ||
| B、πa2-2a2 | ||
C、2a2-
| ||
D、
|
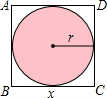如图所示一个正方形的边长是x，圆的半径为r，求图中的空白面积（列代数式）
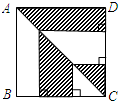如图所示，正方形的边长为8，则阴影部分的面积为
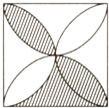如图所示，正方形的边长为a，以各边为直径在正方形内作半圆，求图中阴影部分的面积．