题目内容
观察下列式子:第1个式子:52-42=32;第2个式子:132-122=52
第3个式子:252-242=72;…
按照上述式子的规律,第5个式子为(
第n个式子为
分析:观察发现,右边是奇数列(2n+1)的平方,左边两底数的和等于(2n+1)的平方,差等于1,然后求出两底数即可写出第n个式子,再把n=5代入即可写出第5个式子.
解答:解:根据规律,设第n个式子是x2-y2=(2n+1)2,
则
,
解得
,
∴(2n2+2n+1)2-(2n2+2n)2=(2n+1)2,
第5个式子为:(2×52+2×5+1)2-(2×52+2×5)2=(2×5+1)2,
即612-602=112;
故答案为:612-602=112,(2n2+2n+1)2-(2n2+2n)2=(2n+1)2.
则
|
解得
|
∴(2n2+2n+1)2-(2n2+2n)2=(2n+1)2,
第5个式子为:(2×52+2×5+1)2-(2×52+2×5)2=(2×5+1)2,
即612-602=112;
故答案为:612-602=112,(2n2+2n+1)2-(2n2+2n)2=(2n+1)2.
点评:本题利用平方差公式考查了数字变化规律的问题,求出左边两底数是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目

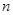 个(
个( ,且
,且 个(
个( ,且
,且