题目内容
如图，一架25米的梯子AB靠在一座建筑物AO上，梯子的底部B距离建筑物AO的底部O有7米（即BO=7米），如果梯子顶部A下滑4米至A1，则梯子底部B滑开的距离BB1是
- A.4米
- B.大于4米
- C.小于4米
- D.无法计算
B
分析：找出直角三角形△OAB，△OA1B1，在直角△OAB中用勾股定理计算OA，在直角三角形OA1B1中，已知AB，OA1根据勾股定理，计算OB1的大小，BB1=OB1-OB．
解答：在直角△OAB中，AB=25，当BO=7时，AO=
=24米，
当下滑4米到A1点时，即OA1=20米，
∴OB1=
=15米，
而OB=7米，所以BB1=8米，大于4米，
故本题答案为大于4米，
故选B．
点评：解决此类问题的关键是找出可以运用勾股定理的直角三角形求解．
分析：找出直角三角形△OAB，△OA1B1，在直角△OAB中用勾股定理计算OA，在直角三角形OA1B1中，已知AB，OA1根据勾股定理，计算OB1的大小，BB1=OB1-OB．
解答：在直角△OAB中，AB=25，当BO=7时，AO=
=24米，当下滑4米到A1点时，即OA1=20米，
∴OB1=
=15米，而OB=7米，所以BB1=8米，大于4米，
故本题答案为大于4米，
故选B．
点评：解决此类问题的关键是找出可以运用勾股定理的直角三角形求解．
练习册系列答案
相关题目
一架方梯AB长25米，如图所示，斜靠在一面墙上：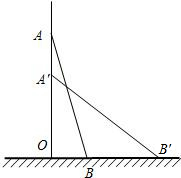
一架方梯长25米，如图，斜靠在一面墙上，梯子底端离墙7米．
一架方梯AB长25米，如图所示，斜靠在一面墙上：