题目内容
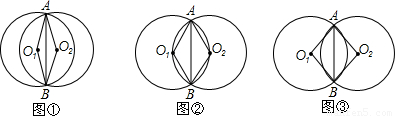
如图①、②、③是两个半径都等于2的⊙O1和⊙O2,由重合状态沿水平方向运动到互相外切过程中的三个位置,⊙O1和⊙O2相交于A、B两点,分别连接O1A、O1B、O2A、O2B和AB.(1)如图②,当∠AO1B=120°时,求两圆重叠部分图形的周长l;
(2)设∠AO1B的度数为x,两圆重叠部分图形的周长为y,求y关于x的函数关系式,并写出自变量x的取值范围;
(3)由(2),若y=2π,则线段O2A所在的直线与⊙O1有何位置关系,为什么?除此之外,它们还有其它的位置关系,写出其它位置关系时x的取值范围.(奖励提示:如果你还能解决下列问题,将酌情另加1~5分,并计入总分.)
在原题的条件下,设∠AO1B的度数为2n,可以发现有些图形的面积S也随∠AO1B变化而变化,试求出其中一个S与n的关系式,并写出n的取值范围.
【答案】分析:(1)根据圆的对称性,该图形的周长是一条弧长的2倍,根据弧长公式计算;
(2)只需把圆心角换成x°即可计算;
(3)根据(2)中的关系式,计算出x的值,根据四边形的形状即可分析判定直线和圆的位置关系.
解答:解:(1)如图②由题意知
解法一:依对称性得,∠AO2B=∠AO1B=120°,
∴l=2×[ ×(2π×2)]=
×(2π×2)]=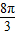 ,
,
解法二:∵O1A=O1B=O2A=O2B,
∴四边形AO1BO2是菱形,
∴∠AO2B=∠AO1B=120°,
∴l=2×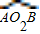 的长=
的长=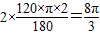 ;
;
(2)由(1)知菱形AO1BO2中∠AO2B=∠AO1B,且度数都是x,
∴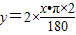 ,
,
得y=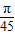 x(0≤x≤180);
x(0≤x≤180);
(3)若y=2π,则线段O2A所在直线与圆O1相切,
因为y=2π,由(2)知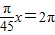 ,
,
解得x=90,
∴∠AO1B=90°,知菱形AO1BO2是正方形,
∴∠O1AO2=90°,即O2A⊥O1A,
而O1A是圆O1的半径,且点A为O1A的外端,
∴线段O2A所在的直线与圆O1相切.
还有线段O2A所在的直线与圆O1相交,此时0≤x<90和90<x≤180,
如:扇形O1AB的面积:S=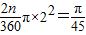 n(0≤n≤90);
n(0≤n≤90);
△O1AB的面积:S=4sinn°cosn°(0≤n≤90);
半重叠部分图形的面积:S=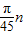 -4sinn°cosn°(0≤n≤90).
-4sinn°cosn°(0≤n≤90).
点评:熟练运用弧长公式进行计算.熟悉切线的判定方法,能够根据直线和圆相切进一步讨论其它情况.
(2)只需把圆心角换成x°即可计算;
(3)根据(2)中的关系式,计算出x的值,根据四边形的形状即可分析判定直线和圆的位置关系.
解答:解:(1)如图②由题意知
解法一:依对称性得,∠AO2B=∠AO1B=120°,
∴l=2×[
 ×(2π×2)]=
×(2π×2)]=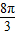 ,
,解法二:∵O1A=O1B=O2A=O2B,
∴四边形AO1BO2是菱形,
∴∠AO2B=∠AO1B=120°,
∴l=2×
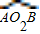 的长=
的长=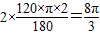 ;
;(2)由(1)知菱形AO1BO2中∠AO2B=∠AO1B,且度数都是x,
∴
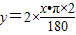 ,
,得y=
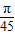 x(0≤x≤180);
x(0≤x≤180);(3)若y=2π,则线段O2A所在直线与圆O1相切,
因为y=2π,由(2)知
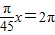 ,
,解得x=90,
∴∠AO1B=90°,知菱形AO1BO2是正方形,
∴∠O1AO2=90°,即O2A⊥O1A,
而O1A是圆O1的半径,且点A为O1A的外端,
∴线段O2A所在的直线与圆O1相切.
还有线段O2A所在的直线与圆O1相交,此时0≤x<90和90<x≤180,
如:扇形O1AB的面积:S=
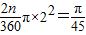 n(0≤n≤90);
n(0≤n≤90);△O1AB的面积:S=4sinn°cosn°(0≤n≤90);
半重叠部分图形的面积:S=
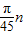 -4sinn°cosn°(0≤n≤90).
-4sinn°cosn°(0≤n≤90).点评:熟练运用弧长公式进行计算.熟悉切线的判定方法,能够根据直线和圆相切进一步讨论其它情况.

练习册系列答案
相关题目
 25、如图a,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE.
25、如图a,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE.
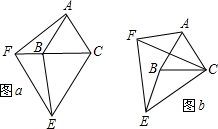 F和BE
F和BE