题目内容
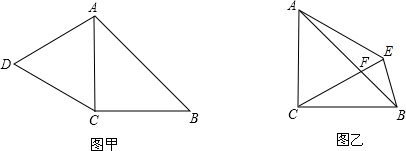
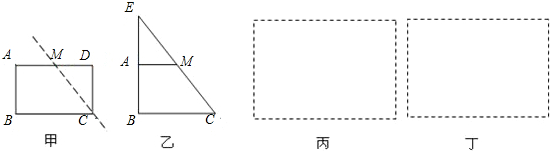
图形F1是等腰直角三角形．以它的直角顶点为旋转中心，把F1沿同一方向依次旋转90°，180°，270°，分别得到图形F2、F3和F4，则F1、F2、F3和F4组成的几何图形是（ ）
分析：设F1是等腰直角△OAB，易证F1、F2、F3和F4组成的四边形四角是直角，且四边相等，据此即可判断．
解答：
解：设F1是等腰直角△OAB，
则∠ABO=∠BAO=45°，
进行第一次旋转，A旋转到B的位置，B旋转到C的位置，
则∠OBC=∠BAO=45°，
∴∠ABC=90°，
同理，可得旋转后得到的四边形四个角都是直角，
又∵根据旋转的性质可得四边相等．
∴F1、F2、F3和F4组成的几何图形是正方形．
故选A．
解：设F1是等腰直角△OAB，则∠ABO=∠BAO=45°，
进行第一次旋转，A旋转到B的位置，B旋转到C的位置，
则∠OBC=∠BAO=45°，
∴∠ABC=90°，
同理，可得旋转后得到的四边形四个角都是直角，
又∵根据旋转的性质可得四边相等．
∴F1、F2、F3和F4组成的几何图形是正方形．
故选A．
点评：本题考查了正方形的判定以及旋转的性质，理解旋转过程中的相等的角以及相等的线段是关键．
练习册系列答案
阅读快车系列答案
相关题目
已知一次函数y=ax+b的图象经过点（0，1），它与坐标轴围成的图形是等腰直角三角形，则a的值为（ ）
| A、1 | B、-1 | C、±1 | D、不确定 |