题目内容
【题目】如图，AB是⊙O的直径，弦CD⊥AB于点E，∠CDB=30°，CD=2 
，则阴影部分的面积为 ． 
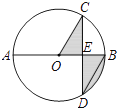
【答案】
【解析】解：连接OD．
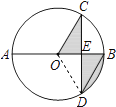
∵CD⊥AB，
∴CE=DE= 
CD= 
（垂径定理），
故S△OCE=S△ODE，
即可得阴影部分的面积等于扇形OBD的面积，
又∵∠CDB=30°，
∴∠COB=60°（圆周角定理），
∴OC=2，
故S扇形OBD= 
= ，即阴影部分的面积为 ．
所以答案是： ．
【考点精析】根据题目的已知条件，利用垂径定理和扇形面积计算公式的相关知识可以得到问题的答案，需要掌握垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．
练习册系列答案
走进文言文系列答案
相关题目
【题目】随着“互联网+”时代的到来，一种新型打车方式受到大众欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按x元/公里计算，耗时费按y元/分钟计算（总费用不足9元按9元计价）．小明、小刚两人用该打车方式出行，按上述计价规则，其打车总费用、行驶里程数与打车时间如表：
时间（分钟） | 里程数（公里） | 车费（元） | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
（1）求x，y的值；
（2）如果小华也用该打车方式，打车行驶了11公里，用了14分钟，那么小华的打车总费用为多少？