题目内容
已知正方形的一条对角线长为4cm，则它的面积是 cm2．
【答案】分析：根据正方形性质可知：正方形的一条角平分线即为对角线，对角线和正方形的两条相邻的边构成等腰直角三角形，根据勾股定理可知正方形的边长，进而可得这个正方形的面积．
解答：解：设这个正方形的边长为xcm，
则根据正方形的性质可知：x2+x2=42=16，
解可得x=2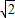
cm；
则它的面积是x2=8cm2，
故答案为8cm2．
点评：主要考查到正方形的性质和面积的求法．要注意：正方形的对角线和正方形的两条相邻的边构成等腰直角三角形．
解答：解：设这个正方形的边长为xcm，
则根据正方形的性质可知：x2+x2=42=16，
解可得x=2
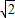cm；则它的面积是x2=8cm2，
故答案为8cm2．
点评：主要考查到正方形的性质和面积的求法．要注意：正方形的对角线和正方形的两条相邻的边构成等腰直角三角形．
练习册系列答案
阅读快车系列答案
相关题目
，高为________cm．
，一边与一条对角线的比为3∶5，则矩形的对角线长是________cm．
，高为________cm．
，一边与一条对角线的比为3∶5，则矩形的对角线长是________cm．