Question

【题目】如图，在平面直角坐标系中，点坐标为，点从点出发以1个单位长度/秒的速度沿轴正半轴方向运动，同时，点从点出发以1个单位长度/秒的速度沿轴负半轴方向运动，设点、运动的时间为秒.以为斜边，向第一象限内作等腰，连接.下列四个说法：

①；②点坐标为；③四边形的面积为16；④.其中正确的说法个数有（ ）

A.4B.3C.2D.1

Answer 1

【答案】B

【解析】

根据题意，有OP=AQ，即可得到，①正确；当时，OP=OQ=4，此时四边形PBQO是正方形，则PB=QB=OP=OQ=4，即点B坐标为（4，4），②正确；四边形PBQO的面积为：，在P、Q运动过程面积没有发生变化，故③正确；由正方形PBQO的性质，则此时对角线PQ=OB，故④错误；即可得到答案.

解：根据题意，点P与点Q同时以1个单位长度/秒的速度运动，

∴OP=AQ，

∵OQ+AQ=OA=8，

∴OQ+OP=8，①正确；

由题意，点P与点Q运动时，点B的位置没有变化，四边形PBQO的面积没有变化，

当时，如图：

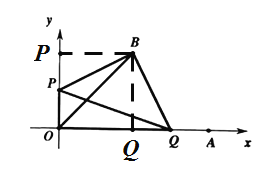
则AQ=OP=4，

∴OQ=，

∴点B的坐标为：（4，4），②正确；

此时四边形PBQO是正方形，则PB=QB=OP=OQ=4，

∴四边形PBQO的面积为：，③正确；

∵四边形PBQO是正方形，

∴PQ=OB，

即当时，PQ=OB，故④错误；

∴正确的有：①②③，共三个；

故选择：B.