题目内容
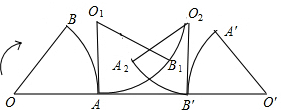（2013•梧州模拟）如图，已知扇形的圆心角为60°，半径为1，将它沿着箭头方向无滑动滚动到O′A′B′位置，则有：①点O到O′的路径是OO1→O1O2→O2O′；
②点O到O′的路径是
 |
| OO1 |
|
| O1O2 |
|
| O2O′ |
③点O在O1→O2段上的运动路径是线段O1O2；
④点O到O′所经过的路径长为
| 4 |
| 3 |
以上命题正确的序号是（ ）
分析：根据旋转的性质对点O到O′所经过的路径分三段分析求解即可．
解答：解：点O到O1，是以A为圆心，以OA长为半径的90°弧长，
从O1到O2是圆的滚动，路径长为AB′的长度，
从O2到O′是以B′为圆心，以OB长为半径的90°弧长，
所以，①点O到O′的路径是OO1→O1O2→O2O′，错误；
②点O到O′的路径是
→
→
，错误；
③点O在O1→O2段上的运动路径是线段O1O2，正确，
④点O到O′所经过的路径长为：
+
+
=
π，正确．
综上所述，正确的有③④．
故选B．
从O1到O2是圆的滚动，路径长为AB′的长度，
从O2到O′是以B′为圆心，以OB长为半径的90°弧长，
所以，①点O到O′的路径是OO1→O1O2→O2O′，错误；
②点O到O′的路径是
|
| OO1 |
|
| O1O2 |
|
| O2O′ |
③点O在O1→O2段上的运动路径是线段O1O2，正确，
④点O到O′所经过的路径长为：
| 90•π•1 |
| 180 |
| 60•π•1 |
| 180 |
| 90•π•1 |
| 180 |
| 4 |
| 3 |
综上所述，正确的有③④．
故选B．
点评：本题考查了旋转的性质，弧长的计算，根据题意，准确分析得到三段的运动过程是解题的关键．
练习册系列答案
相关题目
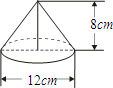（2013•梧州模拟）如图，一个圆锥形零件，高为8cm，底面圆的直径为12cm，则此圆锥的侧面积是（ ）
（2013•梧州模拟）一个边长为4的等边三角形ABC的高与⊙O的直径相等，如图放置，⊙O与BC相切于点C，⊙O与AC相交于点E，则CE的长是（ ）