题目内容
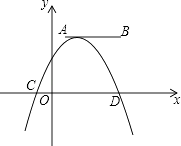
【题目】如图，在平面直角坐标系中，直线l：y1=2x+4，与y轴交于点A，与x轴交于点B，反比例函数y2= 
与直线l交于点C，且AB=2AC． 
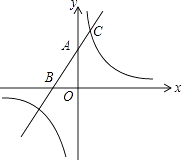
（1）求反比例函数的解析式；
（2）根据函数图象，直接写出0＜y1＜y2的x的取值范围．
【答案】
（1）解：如图，过点C作CH⊥y轴，垂足为H．
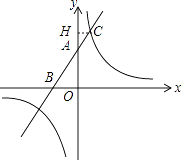
把x=0代入y1=2x+4得，y=4，
把y=0，代入y1=2x+4得，x=﹣2，
∴A点坐标为（0，4），B点坐标为（﹣2，0），
∴OB=2，OA=4，
∵OB∥CH，
∴△ABO∽△ACH
∴ 
，
即 
，
解得AH=2，CH=1，
∴OH=6
∴点C坐标为（1，6）
把点C作标代入反比例函数解析式，得k=6
∴反比例函数的解析式为y= 
（2）解：∵点C坐标（1，6），
∴由图象可知，0＜y1＜y2解析时，0＜x＜1．
【解析】由OB∥CH得△ABO∽△ACH得 ，由此可以求出点P坐标．
练习册系列答案
相关题目
