题目内容
如图1,四边形ABCD、DEFG都是正方形,且C、D、E在同一条直线上,连接AE、CG.

(1)猜想AE与CG的数量关系和位置关系,并给予说明.
(2)把正方形ABCD绕点D旋转到如图2所示的位置,上述结论还成立吗?若成立,请给予证明;若不成立,请说明理由.

(1)猜想AE与CG的数量关系和位置关系,并给予说明.
(2)把正方形ABCD绕点D旋转到如图2所示的位置,上述结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
考点:正方形的性质,全等三角形的判定与性质,旋转的性质
专题:
分析:(1)根据正方形的性质可得AD=CD,DE=DG,∠ADC=∠GDE=90°,然后利用“边角边”证明△ADE和△CDG全等,根据全等三角形对应边相等可得AE=CG,全等三角形对应角相等可得∠CGD=∠AED,延长AE交CG于M,根据∠CGD+∠DCG=90°求出∠AED+∠DCG=90°,然后求出∠CME=90°,再根据垂直的定义即可得解;
(2)根据正方形的性质可得AD=CD,DE=DG,∠ADC=∠GDE=90°,然后求出∠ADE=∠CDG,然后利用“边角边”证明△ADE和△CDG全等,根据全等三角形对应边相等可得AE=CG,全等三角形对应角相等可得∠CGD=∠AED,延长AE交CG于M,延长GC交ED的延长线于N,根据∠CGD+∠N=90°求出∠AED+∠N=90°,然后求出∠CME=90°,再根据垂直的定义即可得解.
(2)根据正方形的性质可得AD=CD,DE=DG,∠ADC=∠GDE=90°,然后求出∠ADE=∠CDG,然后利用“边角边”证明△ADE和△CDG全等,根据全等三角形对应边相等可得AE=CG,全等三角形对应角相等可得∠CGD=∠AED,延长AE交CG于M,延长GC交ED的延长线于N,根据∠CGD+∠N=90°求出∠AED+∠N=90°,然后求出∠CME=90°,再根据垂直的定义即可得解.
解答:解:(1)AE=CG,AE⊥CG.
理由如下:∵四边形ABCD、DEFG都是正方形,
∴AD=CD,DE=DG,∠ADC=∠GDE=90°,
∵在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠CGD=∠AED,
延长AE交CG于M,
∵∠CGD+∠DCG=90°,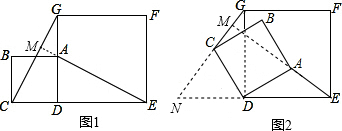
∴∠AED+∠DCG=90°,
∴∠EMC=180°-(∠AED+∠DCG)=180°-90°=90°,
∴AE⊥CG;
(2)结论还成立.
理由如下:∵四边形ABCD、DEFG都是正方形,
∴AD=CD,DE=DG,∠ADC=∠GDE=90°,
∴∠ADC-∠ADG=∠GDE-∠ADG,
即∠ADE=∠CDG,
∵在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠CGD=∠AED,
延长AE交CG于M,延长GC交ED的延长线于N,
∵∠CGD+∠N=90°,
∴∠AED+∠N=90°,
∴∠EMN=180°-(∠AED+∠N)=180°-90°=90°,
∴AE⊥CG.
理由如下:∵四边形ABCD、DEFG都是正方形,
∴AD=CD,DE=DG,∠ADC=∠GDE=90°,
∵在△ADE和△CDG中,
|
∴△ADE≌△CDG(SAS),
∴AE=CG,∠CGD=∠AED,
延长AE交CG于M,
∵∠CGD+∠DCG=90°,

∴∠AED+∠DCG=90°,
∴∠EMC=180°-(∠AED+∠DCG)=180°-90°=90°,
∴AE⊥CG;
(2)结论还成立.
理由如下:∵四边形ABCD、DEFG都是正方形,
∴AD=CD,DE=DG,∠ADC=∠GDE=90°,
∴∠ADC-∠ADG=∠GDE-∠ADG,
即∠ADE=∠CDG,
∵在△ADE和△CDG中,
|
∴△ADE≌△CDG(SAS),
∴AE=CG,∠CGD=∠AED,
延长AE交CG于M,延长GC交ED的延长线于N,
∵∠CGD+∠N=90°,
∴∠AED+∠N=90°,
∴∠EMN=180°-(∠AED+∠N)=180°-90°=90°,
∴AE⊥CG.
点评:本题考查了正方形的性质,全等三角形的判定与性质,以及垂直的定义,熟记正方形的性质确定出三角形全等的条件是解题的关键.

练习册系列答案
相关题目
供电局的电力维修工要到30千米远的郊区进行电力抢修,技术工人小王骑摩托车先走15分钟后,抢修车装载着所需材料才出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,若设摩托车的速度为x千米/小时,则根据题意可得方程( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列说法正确的是( )
| A、了解浙江卫视《中国好声音-The Voice of China》的收视率情况适合用抽样调查 | ||||
| B、在一个只装有白球和红球的袋中摸球,摸出黑球是不确定事件 | ||||
| C、今年3月份某周,我市每天的最高气温(单位:℃)分别是12,9,10,6,11,12,17,则这组数据的极差是5℃ | ||||
D、如果甲组数据的方差
|
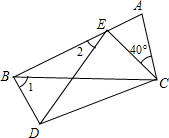 如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=( )
如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=( )| A、90° | B、100° |
| C、110° | D、120° |
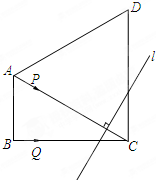 直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=4
直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=4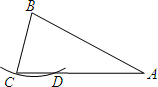 如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为( )
如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为( )
 如图,已知点A(1,y1)、B(2,y2)是反比例函数y=
如图,已知点A(1,y1)、B(2,y2)是反比例函数y=