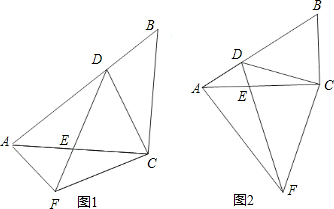
题目内容
点D为Rt△ABC的斜边AB上一点,点E在AC上,连接DE,CD,且∠ADE=∠BCD,CF⊥CD交DE的延长线于点F,连接AF(1)如图1,若AC=BC,求证:AF⊥AB;
(2)如图2,若AC≠BC,当点D在AB上运动时,求证:AF⊥AB.

【答案】分析:(1)根据∠ADE=∠BCD可得出∠FDC=∠B=45°,进而可得到△CDB≌△CAF,由全等三角形的性质即可得出AF⊥AB;
(2)先根据相似三角形的判定定理得出△ACB∽△FDC,进而得出△BCD∽△ACF,再由相似三角形的性质即可得出结论.
解答:证明:(1)∵∠ADE=∠BCD,
∴∠FDC=∠B=45°,
∴CD=CF,
∴△CDB≌△CAF,
∴∠CAF=45°,
∴AF⊥AB;
(2)∵∠ADE=∠BCD,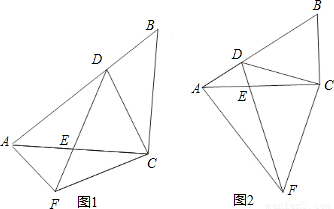
∠ACD+∠DCB=90°,
∠DCA+∠ACF=90°,
∴∠ACF=∠BCD=∠ADF,
∵∠AED=∠CEF,
∴∠BAC=∠CFD,
∵∠ACB=∠DCF=90°,
∴△ACB∽△FDC,
∴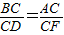 ,
,
∴△BCD∽△ACF,
∴∠B=∠CAF,
∴AF⊥AB.
点评:本题考查的是相似三角形的判定与性质,全等三角形的判定与性质,熟知以上知识是解答此题的关键.
(2)先根据相似三角形的判定定理得出△ACB∽△FDC,进而得出△BCD∽△ACF,再由相似三角形的性质即可得出结论.
解答:证明:(1)∵∠ADE=∠BCD,
∴∠FDC=∠B=45°,
∴CD=CF,
∴△CDB≌△CAF,
∴∠CAF=45°,
∴AF⊥AB;
(2)∵∠ADE=∠BCD,

∠ACD+∠DCB=90°,
∠DCA+∠ACF=90°,
∴∠ACF=∠BCD=∠ADF,
∵∠AED=∠CEF,
∴∠BAC=∠CFD,
∵∠ACB=∠DCF=90°,
∴△ACB∽△FDC,
∴
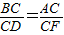 ,
,∴△BCD∽△ACF,
∴∠B=∠CAF,
∴AF⊥AB.
点评:本题考查的是相似三角形的判定与性质,全等三角形的判定与性质,熟知以上知识是解答此题的关键.

练习册系列答案
相关题目