题目内容
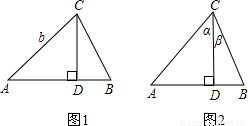
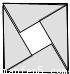
 如图1,由直角三角形边角关系,可将三角形面积公式变形,
如图1,由直角三角形边角关系,可将三角形面积公式变形,即:S△ABC=
| 1 |
| 2 |
在Rt△ACD中,∵sinA=
| CD |
| AC |
∴CD=bsinA
∴S△ABC=
| 1 |
| 2 |
即三角形的面积等于两边之长与夹角正弦之积的一半.
如图2,在△ABC中,CD⊥AB于D,∠ACD=α,∠DCB=β.
∵S△ABC=S△ADC+S△BDC,由公式①,得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即AC×BC×sin(α+β)=AC×CD×sinα+BC×CD×sinβ.②
请你利用直角三角形边角关系,消去②中的AC、BC、CD,只用∠α、∠β、∠α+∠β的正弦或余弦函数表示(直接写出结果).
(1)
sin(α+β)=sinα×cosβ+cosα×sinβ
sin(α+β)=sinα×cosβ+cosα×sinβ
(2)利用这个结果计算:sin75°=
| ||||
| 4 |
| ||||
| 4 |
分析:(1)将②式左右两边同时除以AC×BC,变形后等式右边第一项根据利用余弦函数定义表示出cosβ,第二项利用余弦函数定义表示出cosα,即可得到所求的式子;
(2)将所求式子中的角75°变为45°+30°,由(1)得到的关系式变形,再利用特殊角的三角函数值计算,即可得到所求式子的值.
(2)将所求式子中的角75°变为45°+30°,由(1)得到的关系式变形,再利用特殊角的三角函数值计算,即可得到所求式子的值.
解答:解:(1)∵在Rt△ACD中,cosα=
,在Rt△BCD中,cosβ=
,
∴AC×BC×sin(α+β)=AC×CD×sinα+BC×CD×sinβ左右两边同时除以AC×BC得:
sin(α+β)=
×sinα+
×sinβ,
则sin(α+β)=sinα×cosβ+cosα×sinβ;
(2)sin75°=sin(45°+30°)
=sin45°cos30°+cos45°sin30°
=
×
+
×
=
.
故答案为:(1)sin(α+β)=sinα×cosβ+cosα×sinβ;(2)
| CD |
| AC |
| CD |
| BC |
∴AC×BC×sin(α+β)=AC×CD×sinα+BC×CD×sinβ左右两边同时除以AC×BC得:
sin(α+β)=
| CD |
| BC |
| CD |
| AC |
则sin(α+β)=sinα×cosβ+cosα×sinβ;
(2)sin75°=sin(45°+30°)
=sin45°cos30°+cos45°sin30°
=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||||
| 4 |
故答案为:(1)sin(α+β)=sinα×cosβ+cosα×sinβ;(2)
| ||||
| 4 |
点评:此题考查了解三角形的问题,涉及的知识有:锐角三角函数定义,特殊角的三角函数值,以及等式的基本性质,弄清阅读材料中的信息是解本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 18、如图可以看成由直角三角形旋转所得,旋转角度为
18、如图可以看成由直角三角形旋转所得,旋转角度为 如图1,由直角三角形边角关系,可将三角形面积公式变形,
如图1,由直角三角形边角关系,可将三角形面积公式变形,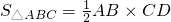 ,
,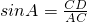 ,
,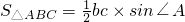 .①
.①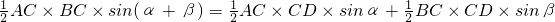 ,
,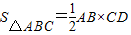 ,
,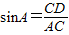 ,
,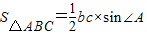 .①
.①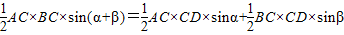 ,
,