题目内容
 已知,如图,P为AB上一点,△APC和△BPD都是等边三角形,求证:AD=BC.
已知,如图,P为AB上一点,△APC和△BPD都是等边三角形,求证:AD=BC.分析:根据等边三角形的性质证明△PCB≌△PAD就可以得出结论.
解答:解:∵△APC和△BPD是等边三角形,
∴AP=CP,DP=BP,∠APC=∠4=60°,
∴∠APC+∠CPD=∠4+∠CPD,即∠APD=∠CPB,
在△PCB≌△PAD中
,
∴△PCB≌△PAD(SAS),
∴AD=BC.
∴AP=CP,DP=BP,∠APC=∠4=60°,
∴∠APC+∠CPD=∠4+∠CPD,即∠APD=∠CPB,
在△PCB≌△PAD中
|
∴△PCB≌△PAD(SAS),
∴AD=BC.
点评:本题考查了等边三角形的性质的运用,全等三角形的判定与性质的运用.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
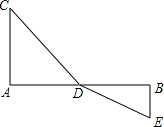 (2013•石景山区一模)问题解决:
(2013•石景山区一模)问题解决: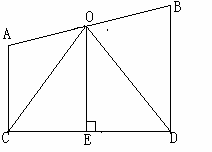

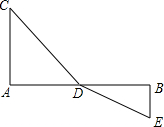 问题解决:
问题解决: 的最小值.
的最小值.