题目内容
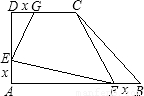
如图所示,已知直角梯形ABCD中,AD∥BC,∠C=∠D=90°,以AB 为直径的⊙O与CD相切于P,若AD=m,BC=n,CD=a.
求证:(1)PC、PD是关于x的方程:x2-ax+mn=0的两根;
(2)a2=4mn.
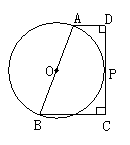
(1)连结OP.∵CD切⊙O于P,∴OP⊥CD,
∵AD⊥CD,BC⊥CD,∴AD∥OP∥BC.
又∵OA=OB,∴PC=PD,
∵CD=a,∴PC+PD=CD=a,
连结PA、PB,∵AB是⊙O 的直径,∴∠APB=90°,∴∠APD+∠BPC=90°,
∵∠D=90°,∴∠APD+∠PAD=90°,∴∠PAD=∠BPC,
又∵∠D=∠C=90°,∴△PAD∽△BPC,
∴![]() ,∴PD·PC=AD·BC.
,∴PD·PC=AD·BC.
∵AD=m,BC= n,∴PD·PC=m·n,
故PC、PD是关于x的方程x2-ax+mn=0的两根.
(2)∵CD=PD+PC,PD=PC,CD=a,∴PC=![]() ,∴PC2=
,∴PC2=![]() ,又PC2=PC·PD,PD·PC=m·n,
,又PC2=PC·PD,PD·PC=m·n,
∴ ![]() =mn,∴a2=4mn.
=mn,∴a2=4mn.
点拨:此题是学科内综合题,是一元二次方程,两三角形相似的识别法,切线的性质及与圆有关的性质的综合应用,通过本题加深了这些知识的联![]() 系和沟通,提高了应用能力.
系和沟通,提高了应用能力.

练习册系列答案
相关题目
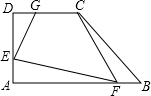 如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4.求四边形CGEF的面积S关于x的函数表达式和x的取值范围.
如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4.求四边形CGEF的面积S关于x的函数表达式和x的取值范围.