题目内容
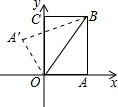 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连OB,将纸片OABC沿OB折叠,使点A落在A′的位置,若OB=
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连OB,将纸片OABC沿OB折叠,使点A落在A′的位置,若OB=| 5 |
| 1 |
| 2 |
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-
|
分析:即求A点关于OB的对称点的坐标.通过解方程组求解.
解答:解:∵tan∠BOC=
,∴OC=2BC.
∵OC2+BC2=OB2=5,∴BC=1,OC=2.
所以A(1,0),B(1,2).
直线OB方程:y-2=2(x-1),
A′和A关于OB对称,假设A′(x0,y0),
AA'中点:x=
,y=
.在直线OB y-2=2(x-1)上,
-2=2(
-1),y0=2(x0+1).
x02+y02=OA'2=OA2=1,
x02+4(x0+1)2=1,
5X02+8X0+3=0.
X0=-1或者-
,
y0=0或者
.
x0=-1,y0=0不合题意,舍去.
所以A(-
,
).
故选C.
| 1 |
| 2 |
∵OC2+BC2=OB2=5,∴BC=1,OC=2.
所以A(1,0),B(1,2).
直线OB方程:y-2=2(x-1),
A′和A关于OB对称,假设A′(x0,y0),
AA'中点:x=
| 1+x0 |
| 2 |
| y0 |
| 2 |
| y0 |
| 2 |
| 1+x0 |
| 2 |
x02+y02=OA'2=OA2=1,
x02+4(x0+1)2=1,
5X02+8X0+3=0.
X0=-1或者-
| 3 |
| 5 |
y0=0或者
| 4 |
| 5 |
x0=-1,y0=0不合题意,舍去.
所以A(-
| 3 |
| 5 |
| 4 |
| 5 |
故选C.
点评:主要考查了坐标与图形的性质,矩形的性质和翻折变换以及三角函数的运用.要熟练掌握才会灵活运用.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
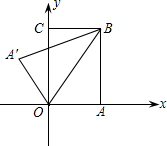 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB将纸片沿OB折叠,使A落在A′的位置,若OB=
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB将纸片沿OB折叠,使A落在A′的位置,若OB= ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 
 ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 

 ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 