题目内容
一辆汽车在公路上匀速行驶,司机在路边看到一个里程碑上是一个两位数,行驶一小时后,他看到的里程碑上的数,恰好是第一个里程碑上数颠倒顺序的两位数,再过一小时,他看到的里程碑上的数,又恰好是第一次看到的两位数中间添上一个零的三位数,那么他第一次看到的两位数是
- A.14
- B.15
- C.16
- D.17
C
分析:设第一次他看到的两位数的个位数为x,十位数为y,汽车行驶速度为v,第一次看到的两位数为10y+x,行驶一小时后看到的两位数为10x+y,第三次看到的三位数为100y+x,由汽车均速行驶可得三段时间的路程相等,即可列出两个方程求解即可.
解答:设第一次他看到的两位数的个位数为x,十位数为y,汽车行驶速度为v,根据题意得:
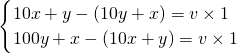 ,
,
解得:x=6y,
∵xy为1-9内的自然数,
∴x=6,y=1;
即两位数为16.
答:他第一次看到的两位数是16.
另法:设个位为x,十位为y,根据题意得:
(10y+x)-(10x+y)=(100x+y)-(10y+x),
x+y=7,
解得:x=1,y=6,
即两位数为16.
答:他第一次看到的两位数是16.
故选C.
点评:本题考查了二元一次方程组的应用,解题关键是弄清题意,合适的等量关系,列出方程组.本题涉及一个常识问题:两位数=10×十位数字+个位数字,并且在求两位数或三位数时,一般是不能直接设这个两位数或三位数的,而是设它各个数位上的数字为未知数.
分析:设第一次他看到的两位数的个位数为x,十位数为y,汽车行驶速度为v,第一次看到的两位数为10y+x,行驶一小时后看到的两位数为10x+y,第三次看到的三位数为100y+x,由汽车均速行驶可得三段时间的路程相等,即可列出两个方程求解即可.
解答:设第一次他看到的两位数的个位数为x,十位数为y,汽车行驶速度为v,根据题意得:
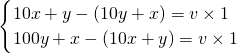 ,
,解得:x=6y,
∵xy为1-9内的自然数,
∴x=6,y=1;
即两位数为16.
答:他第一次看到的两位数是16.
另法:设个位为x,十位为y,根据题意得:
(10y+x)-(10x+y)=(100x+y)-(10y+x),
x+y=7,
解得:x=1,y=6,
即两位数为16.
答:他第一次看到的两位数是16.
故选C.
点评:本题考查了二元一次方程组的应用,解题关键是弄清题意,合适的等量关系,列出方程组.本题涉及一个常识问题:两位数=10×十位数字+个位数字,并且在求两位数或三位数时,一般是不能直接设这个两位数或三位数的,而是设它各个数位上的数字为未知数.

练习册系列答案
相关题目